From the last lecture, we concluded that
- To find the MRI image, we need to determine an amplitude and phase at each point, $k$, in the frequency domain. This amplitude and phase are stored as a complex number.
- To find the amplitude and phase at a particular point, $k$, we induce a gradient integral in the direction of $k$ with magnitude proportional to $|k|$. Then we measure the aggregate moment: its magnitude and its phase shift from the moment at the origin are the amplitude and phase that get stored.
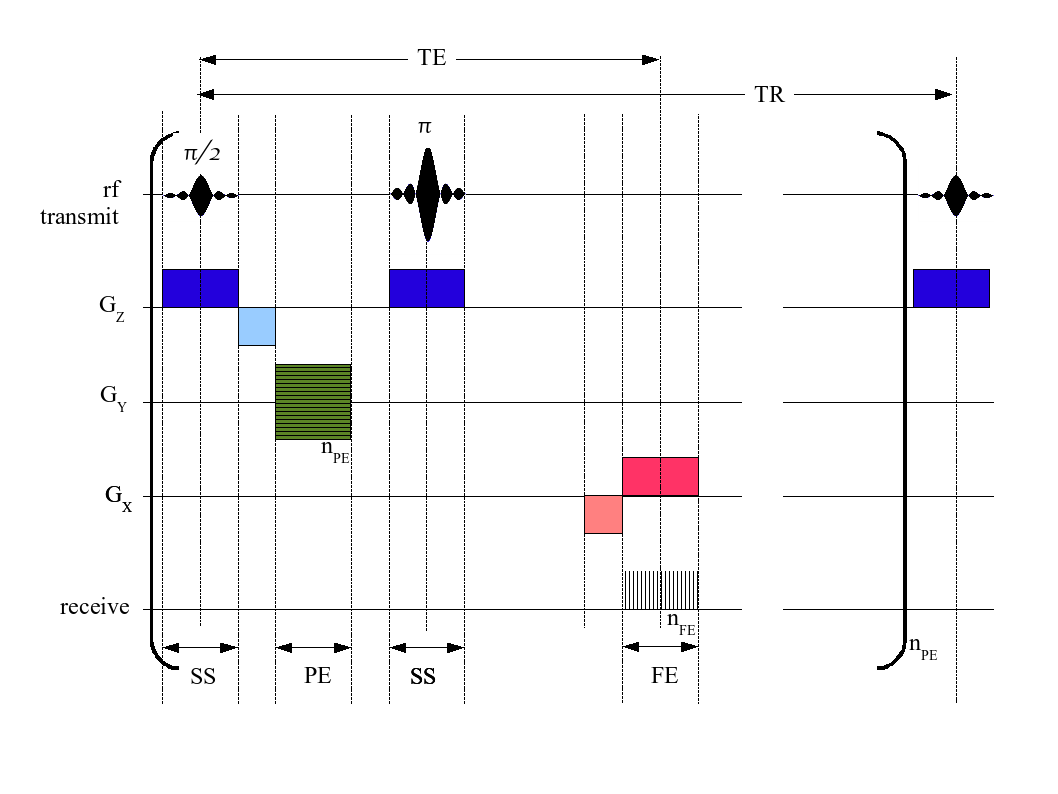
A pulse sequence is a timeline describing the evolution of the various gradients and radiofrequency (RF) transmit and receive operations. Below is a timeline for a spin-echo sequence that reads data for one row in the frequency domain.
- The RF transmit line shows the 90$^o$ pulse (= ${\pi \over 2}$), followed by a 180$^o$ pulse (= $\pi$). This is the classic spin-echo sequence that provides an echo at time TE.
- The $\mathbf{G_z}$ line shows the gradient in the $z$ direction. This is turned on for slice selection (denoted SS at the bottom) during the 90$^o$ and 180$^o$ pulses. Note the negative gradient after the 90$^o$ degree pulse; this rephases the protons within the selected slice. The RF transmit pulse (above) is tuned to transmit in only the frequencies of precession for a chosen transverse slice of the patient.
- The $\mathbf{G_y}$ and $\mathbf{G_x}$ lines show the gradients in the transverse plane. More on these below.
- The receive line shows when the receive coils are measuring the aggregate moment (i.e. the MRI signal).
 [ image from wikipedia ]
[ image from wikipedia ]
The sequence above is repeated once for each horizontal line in the frequency domain. That line has a wavevector $k = (k_x,k_y)$ with constant $k_y$ because it's horizontal.
Each separate line in the frequency domain, $k_y$ is chosen using different amounts of a gradient integral in the $y$ direction. These different amounts are shown as the different horizontal lines in the green box, where $n_\textrm{pe}$ is the number of "phase encoding" (PE) steps. In this pulse sequence, the gradient $G_y$ is turned on for the same duration with each repetition, but its strength varies between repetitions according to which $k_y$ needs to be selected.
The gradient $G_x$ is turned on during the reading of the echo at TE. This has a very interesting and subtle effect:
Over the course of the FE period (named, perhaps confusingly, for "frequency encoding" ... but you should ignore this naming convention), the integral of the gradient in the $x$ direction builds up at a constant rate.
During the FE period, the total integral, $\int G_{xy}\ dt = \int G_x+G_y\ dt$, has a constant component, $\int G_y\ dt$, and a component, $\int G_x\ dt$, that increases linearly with time.
The means that the corresponding wavevector, $k = (k_x,k_y)$, has a constant $k_y$ (corresponding to a horizontal line in the frequency domain) and a steadily increasing $k_x$, which has the effect of "marching" $k$ across that line.
At each position of $k$ on that line, the MRI read coil can measure the aggregate moment's amplitude and phase and record it in the appropriate position within the frequency domain. These positions ($n_\textrm{fe}$ of them) are shown as vertical lines in the FE interval on the "receive" line.
The negative lobe on $G_x$ to the left of the FE interval causes $k$ to move all the way to the left of the line before it starts "marching" from left to right under the influence of the positive gradient.
This pulse sequence requires one TR interval for each row in the frequency domain, so can take quite a long time for large MRI images.
Many, many alternative pulse sequences exist, some of which interleave new pulse sequences while waiting for the TR interval of the first sequence to complete, and others of which traverse the frequency domain in different patterns for faster acquistion or for a reduction in motion artefacts.
Note that it's not just a matter of scanning the frequency domain with different $G_x$ and $G_y$ sequences. We also have to ensure that a signal is present (for example, with spin echo) and ensure that other dephasing effects don't adversely affect the signal. There's a very large body of work on building good pulse sequences.
Commentary
Phase encoding is probably the most difficult thing to understand for newcomers to MRI. It certainly was for me.
This may be due, in part, to the naming of the FE interval as the "frequency encoding" step. Various authors talk about sampling the MR signal at different frequencies during this step, perhaps because the $G_x$ gradient causes different frequencies of precession in the $x$ direction.
However, the sampling is really being done at different, discrete gradient integrals, and each such gradient integral corresponds to a different location, $k$, in the frequency domain.
So the $\mathbf{G_x}$ and $\mathbf{G_y}$ gradients are really only used "build up" a gradient integral, $\mathbf{\int G_{xy}\ dt}$, that selects different wavevectors, $\mathbf{k}$, at which to sample the MR signal.
The use of the $G_z$ gradient to select a slice is completely different and is correctly termed "frequency encoding", since each slice has its own frequency range.