Mutual Information

The $X$ image has some inherent entropy, $H(X)$, and conditional entropy, $H(X|Y)$, if $Y$ is used to predict $X$.

Note that $0 \leq H(X|Y) \leq H(X)$ because knowledge of $Y$ can only provide more information (thus reducing entropy). Knowledge of $Y$ cannot take away information (which would increase entropy).

And $H(X|Y) = H(X)$ when $Y$ provides no information at all about $X$.

So $I(X;Y)$ is in the range $[0,H(X)]$.

$I(X;Y) = 0$ for a terrible registration, while $I(X;Y) = H(X)$ for a perfect registration of identical images.

For an "incoherent" joint histogram, $Y$ will not predict $X$ very well, so we would expect $H(X|Y)$ to be high and $I(X;Y)$ to be close to zero.

As $Y$ better predicts $X$, $H(X|Y)$ diminishes and $I$ increases.

When registering image $Y$ to image $X$ by moving image $Y$ around, $H(X)$ is really a constant, since the image corresponding to $X$ does not change. If your algorithm's goal is to maximize the mutual information, the algorithm can simply minimize $H(X|Y)$.

Here are three registrations of the T1 and T2 images from the previous lecture. The leftmost shows exactly overlapping images with mutual imformation (MI) of 1.5998. The centre shows MI of 1.3465 when the T2 image is shifted 10 pixels up and right. The rightmost shows MI of 1.3247 when the T2 image is further rotated by 13 degrees.

(You can right-click and "view image" to see each of these in detail.)

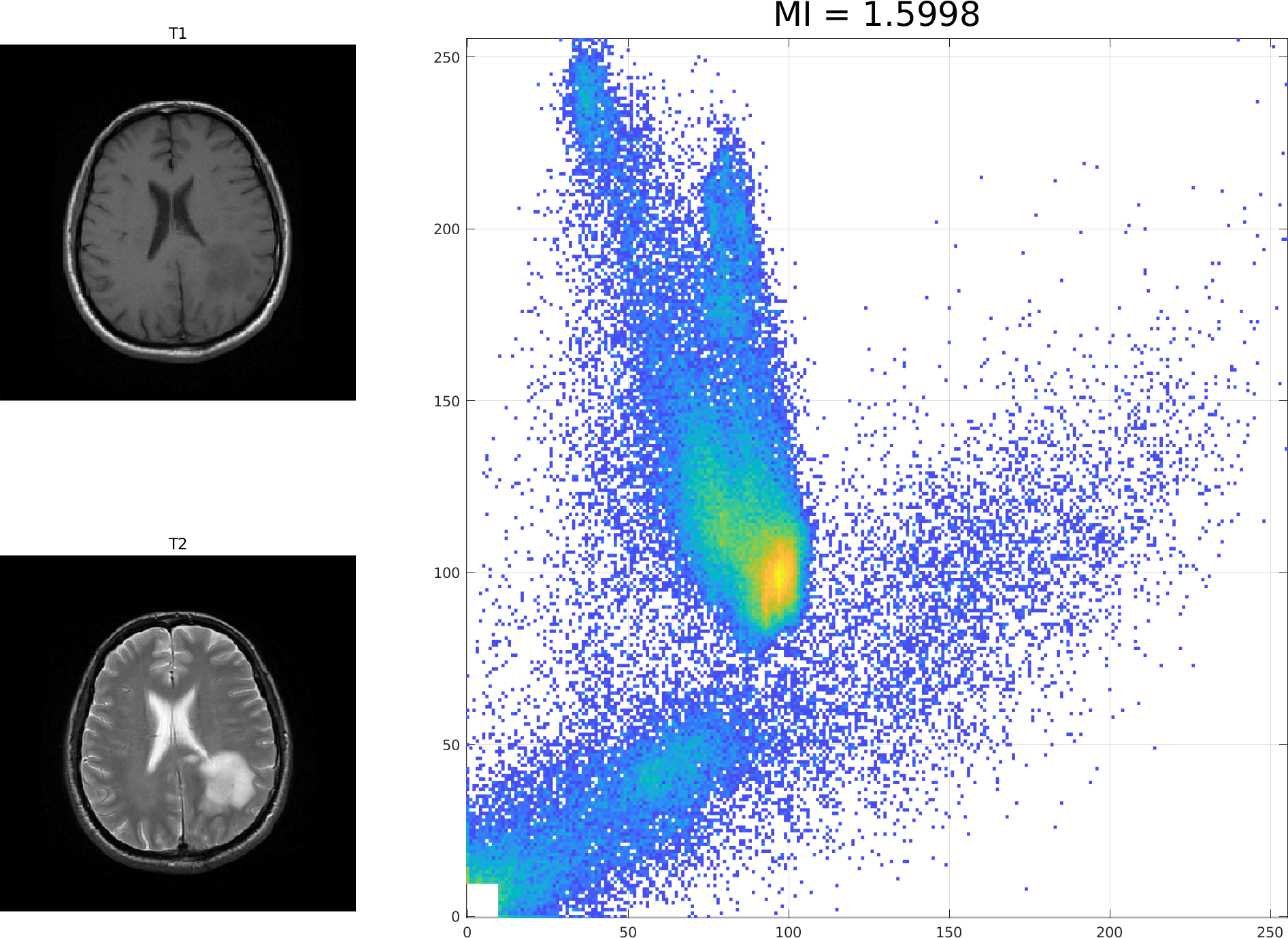
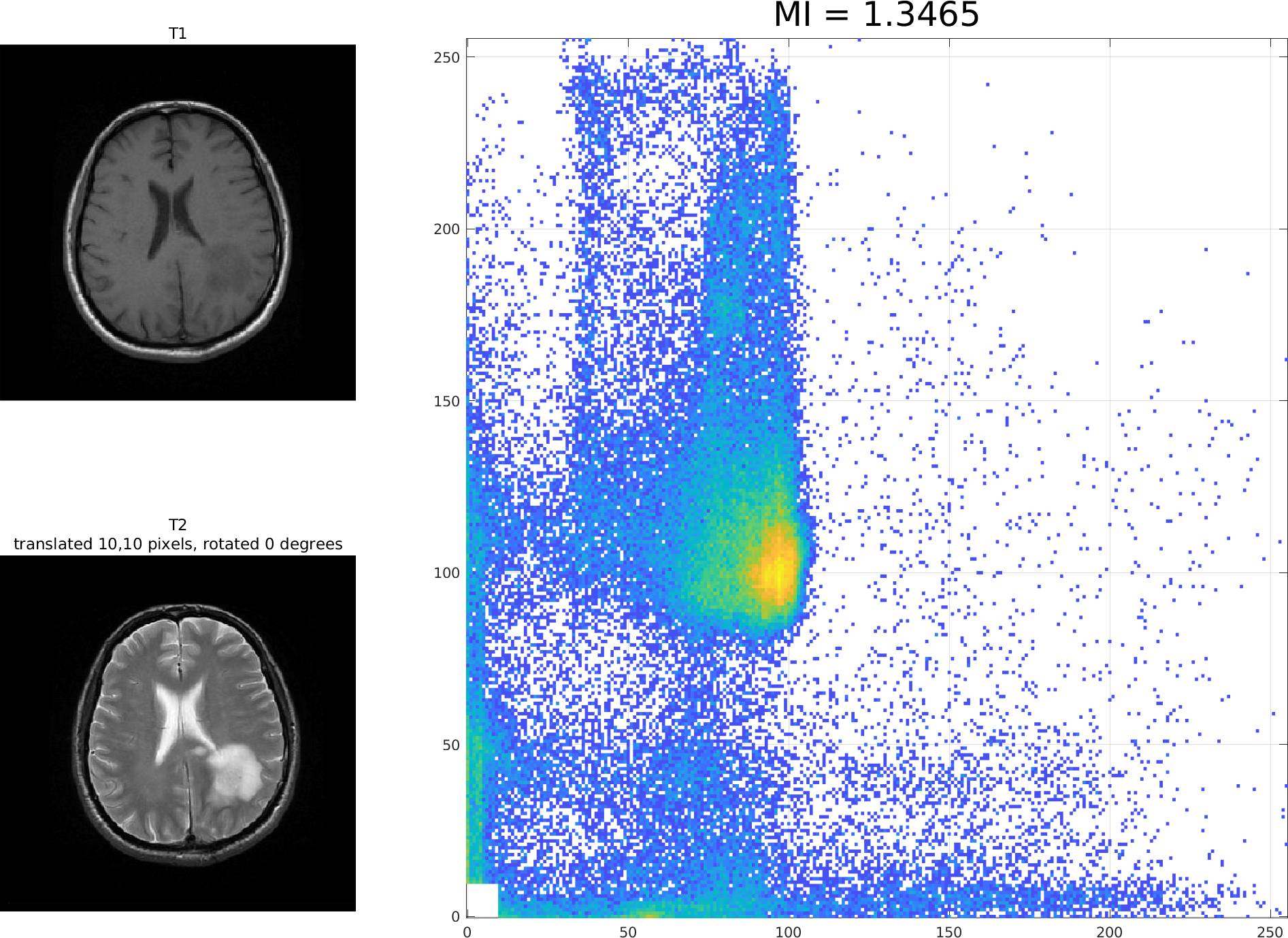
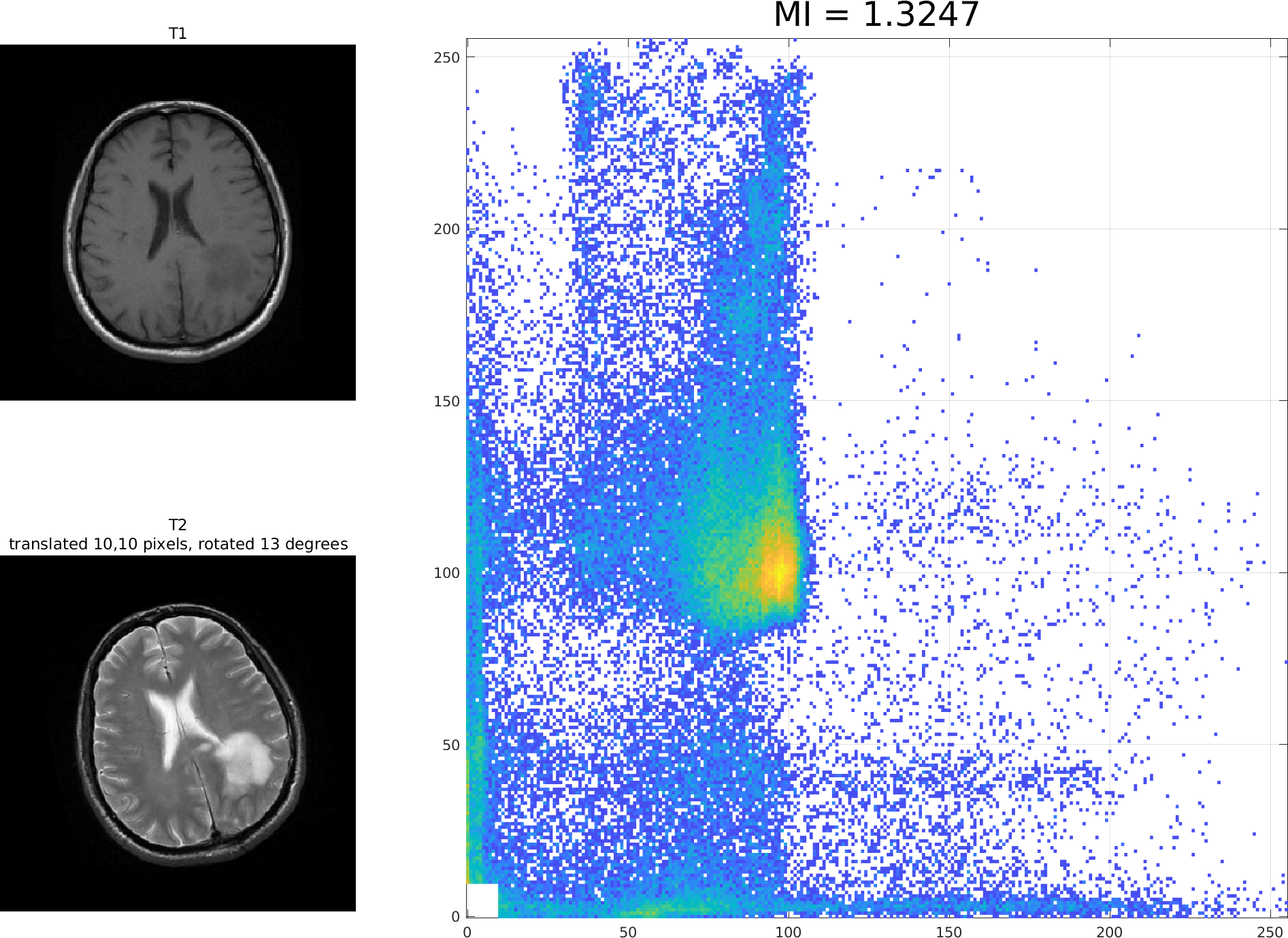
The example above shows how MI decreases as the images become "de-registered".

It can be shown that

$\begin{array}{rl} I(X;Y) & = \sum_{i,j} P_{xy}(i,j) \; \log { P_{xy}(i,j) \over P_x(i) \; P_y(j) } \end{array}$

where $P_{xy}$ is the joint probability distribution, and $P_x$ and $P_y$ are the (so called "marginal") probability distributions of the individual images. The $i$ and $j$ iterate over the range of pixel intensities in each image.

This has a fairly intuitive explanation:

• The outer sum computes the probability-weighted average of the log term, taken over the whole of the joint probability distribution (i.e. all possible pairs of pixel intensities).
• The numerator, $P_{xy}(i,j)$, of the $\log$ term is the probability that a pixel with intensity $i$ in one image will overlap with a pixel of intensity $j$ in the other image.
• The denominator, $P_x(i) \times P_y(j)$, of the $\log$ term is the probability that intensities $i$ and $j$ will overlap if the images were completely independent. That's because $P_x(i) \times P_y(j)$ is the probabilty that $i$ and $j$ are chosen independently.
• So the argument of the $\log$ is the probability of $i$ and $j$ overlapping with a particular registration of the images, divided by the probability that they overlap if they are completely independent. It's how much more likely $i$ and $j$ are to overlap in these overlapping images than in two completely independent images.
• If the argument of the $\log$ term is 1, that means that $i$ and $j$ are equally likely to overlap in the registered images as in two independent images, so $j$ does not help to predict $i$ and $\log 1 = 0$.
• However, if the argument of the $\log$ term is greater than 1, then $\log$ of that is greater than zero and the "mutual information" is increased.

The formula above is probabily the easiest way to compute mutual information from a joint histogram.

MI is good for inter-modal registration because it considers how well each pixel intensity in one image predicts each pixel intensity in another image.

Unlike other similarity measures we've seen, this doesn't require that images be of the same modality. That's because there is no requirement for a monotonic relation between the pixel intensities, in that low intensities in $I_1$ don't have to correspond to low intensities in $I_2$, and high intensities in $I_1$ don't have to correspond to high intensities in $I_2$.

Mutual information tends to have a small "capture radius" in that the MI value doesn't start decreasing to the global minimum until the images are already very closely registered.

The name "mutual information" is used because it is a measure of how much information is shared between the two images or, equivalently, how well each image can predict the other.

A variant, Normalized Mutual Information (NMI), is better in that it is less sensitve to changes in the overlapping area.