A pixel intensity $i_1$ in image $I_1$ is said to predict pixel intensity $i_2$ in image $I_2$ if, when the images overlap, pixels of intensity $i_1$ in $I_1$ usually overlap with pixels of intensity $i_2$ in $I_2$.

The joint histogram (copied below from the last lecture), encapsulates the idea of one pixel intensity predicting another:

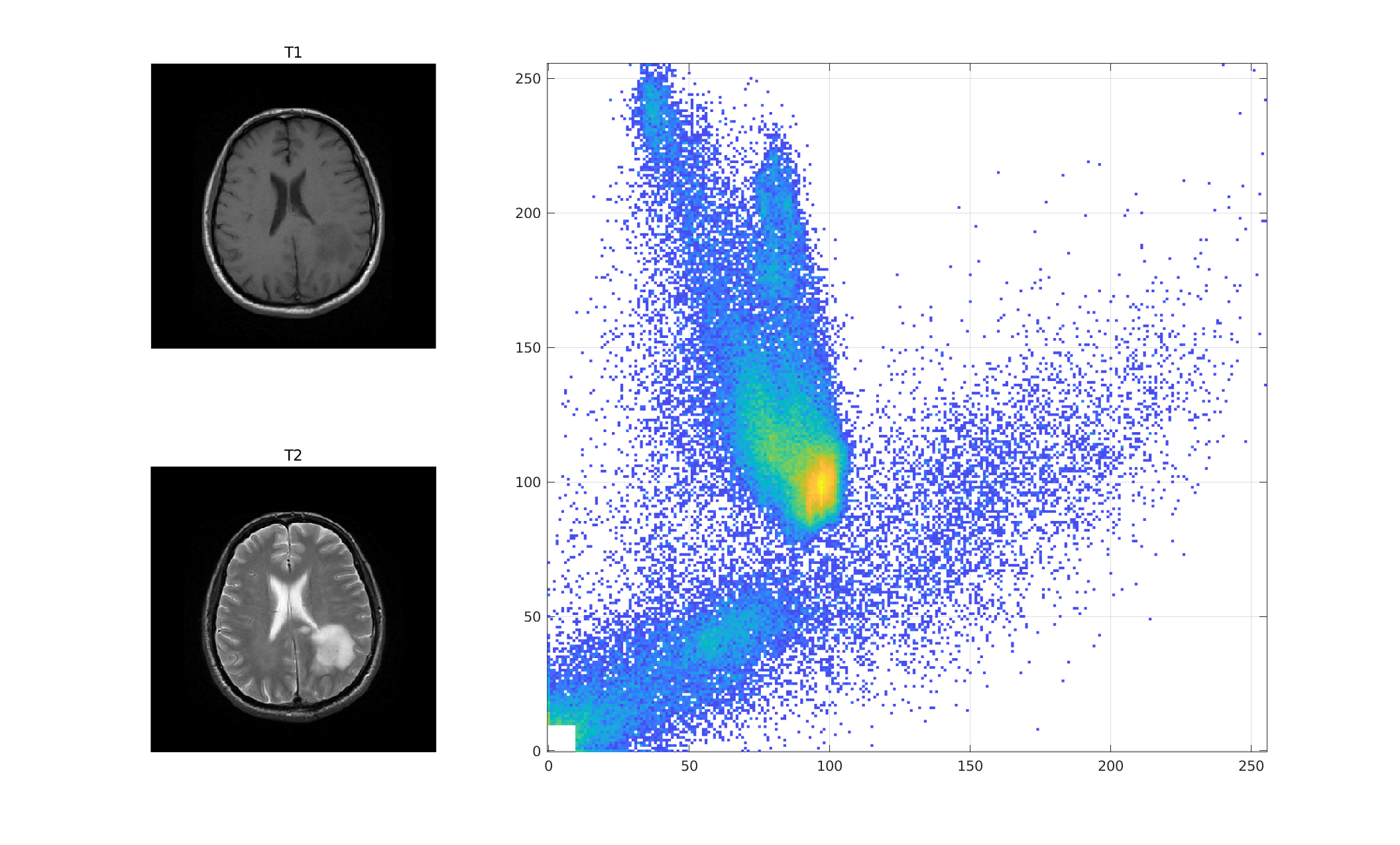
Recall that $h(x,y)$ in this T1/T2 joint histogram shows the number of times that value $x$ in the T1 image and value $y$ in the T2 image occur in the same place (i.e. overlap).

For example, if $h(x,y)$ is bright yellow (above), the intensity $x$ in the T1 image and intensity $y$ the T2 image overlap frequently.

That means that intensity $x$ in T1 predicts intensity $y$ in T2.

Ideally, each intensity $x$ would alway predict a unique and different intensity $y$. Then the joint histogram would have a single peak in each row and in each column.

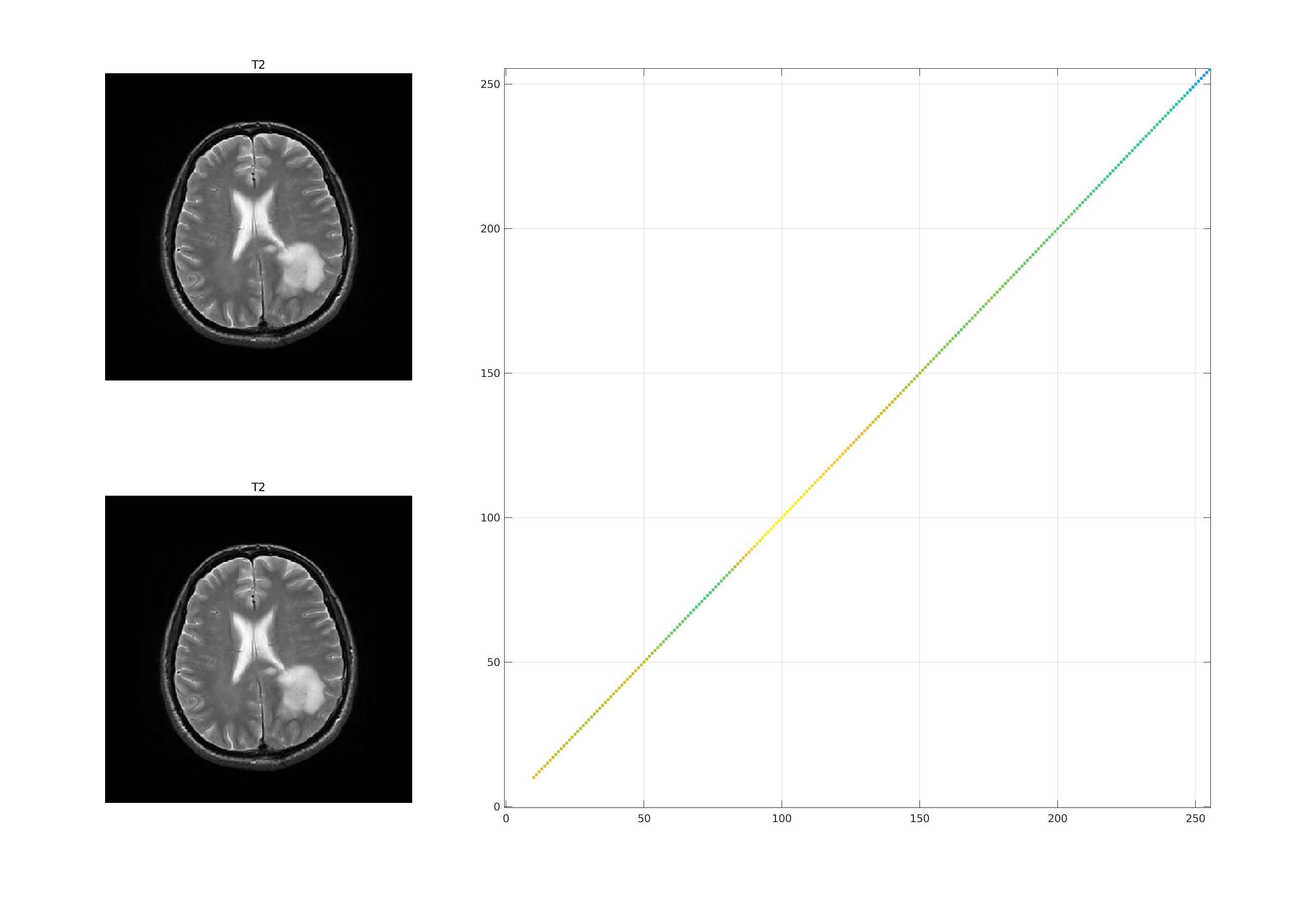
For example, consider an image overlapped with a copy of itself. Then each pixel intensity in the first image predicts exactly one pixel intensity (the same pixel intensity) in the other image, and the joint histogram is a set of peaks along the diagonal, like this:

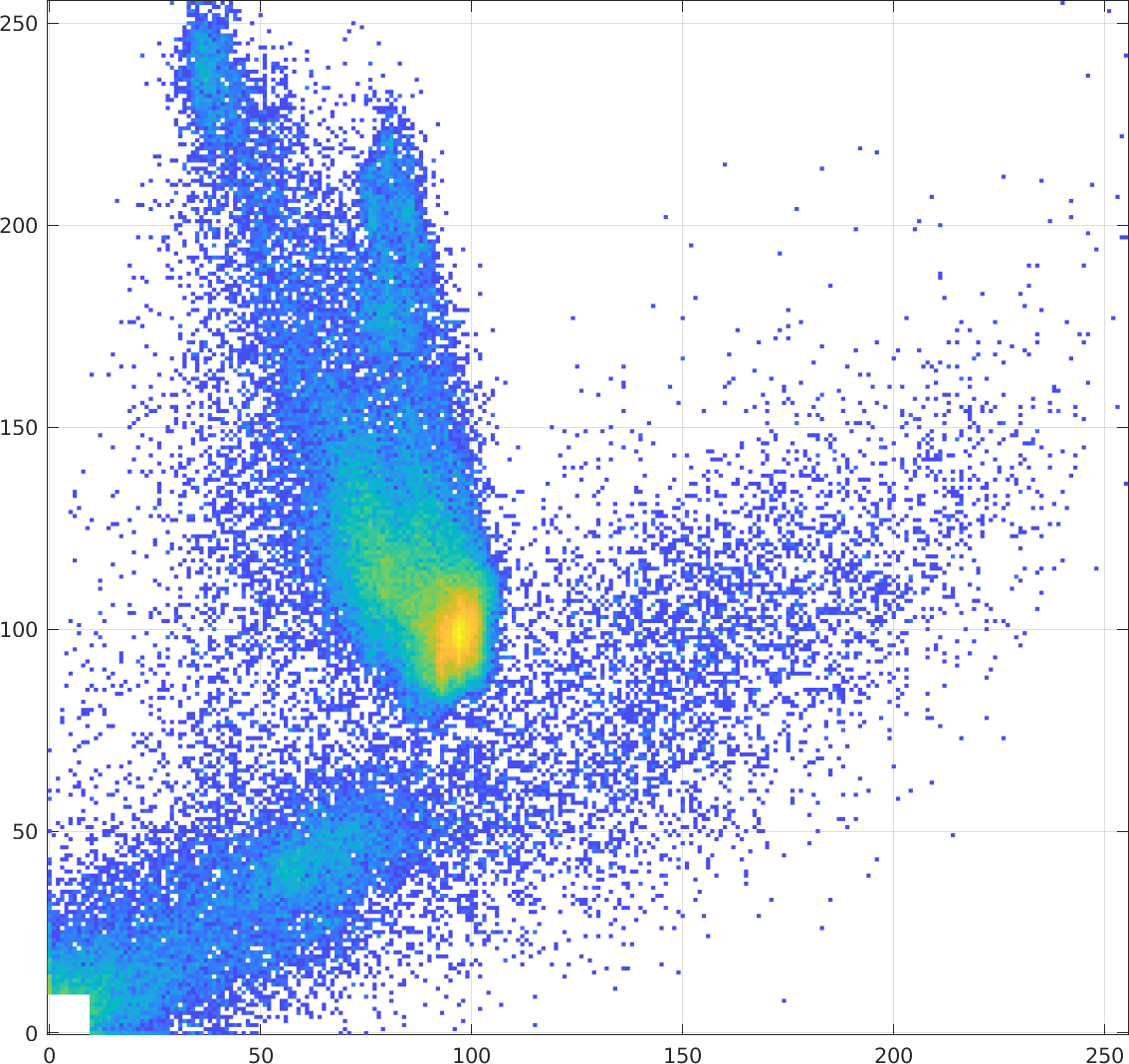
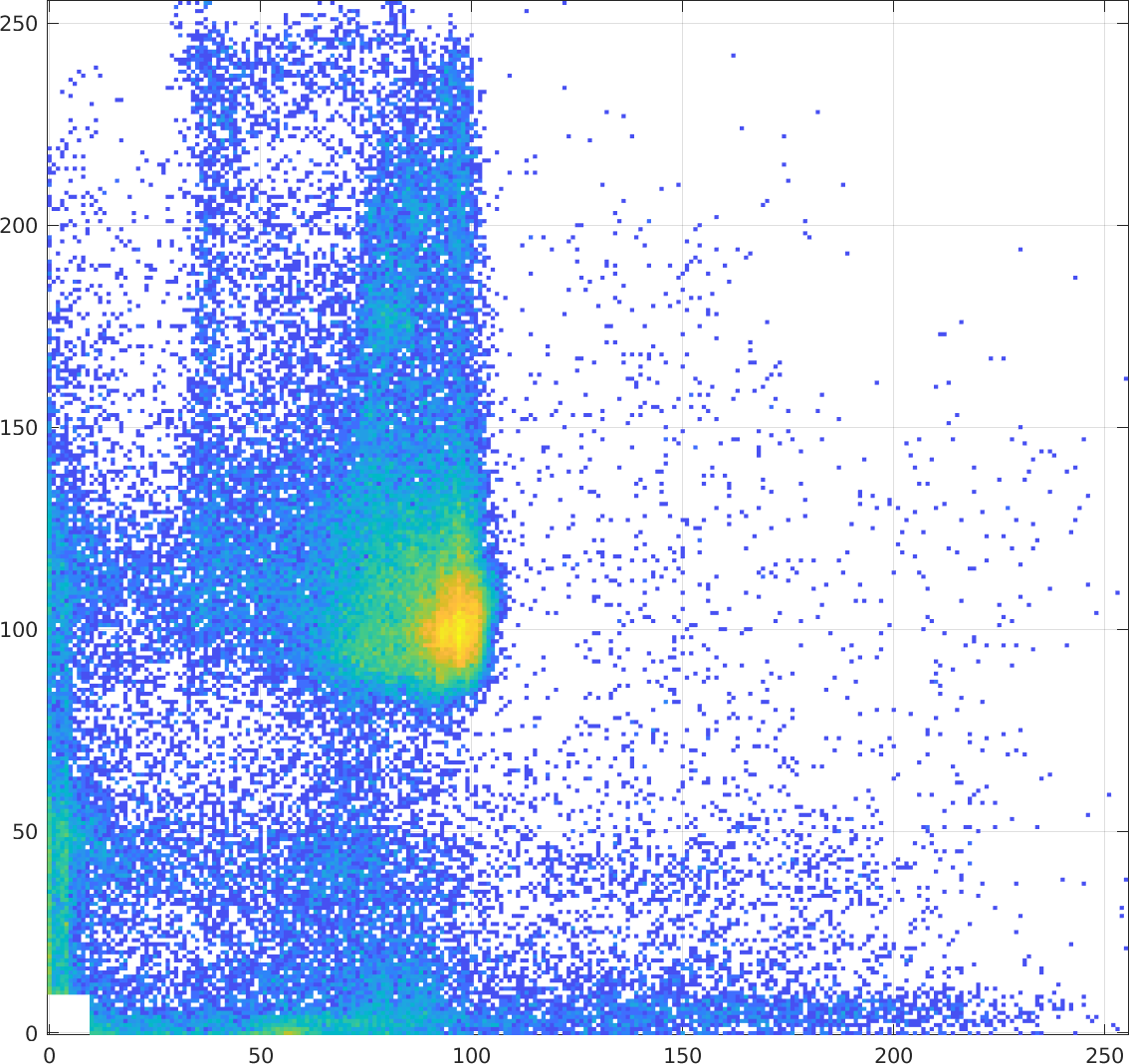
As the above images become "de-registered" by translating and rotating one with respect to the other, the joint histogram becomes less coherent.

Here is the joint histogram with the bottom T2 image translated 2 pixels to the right:

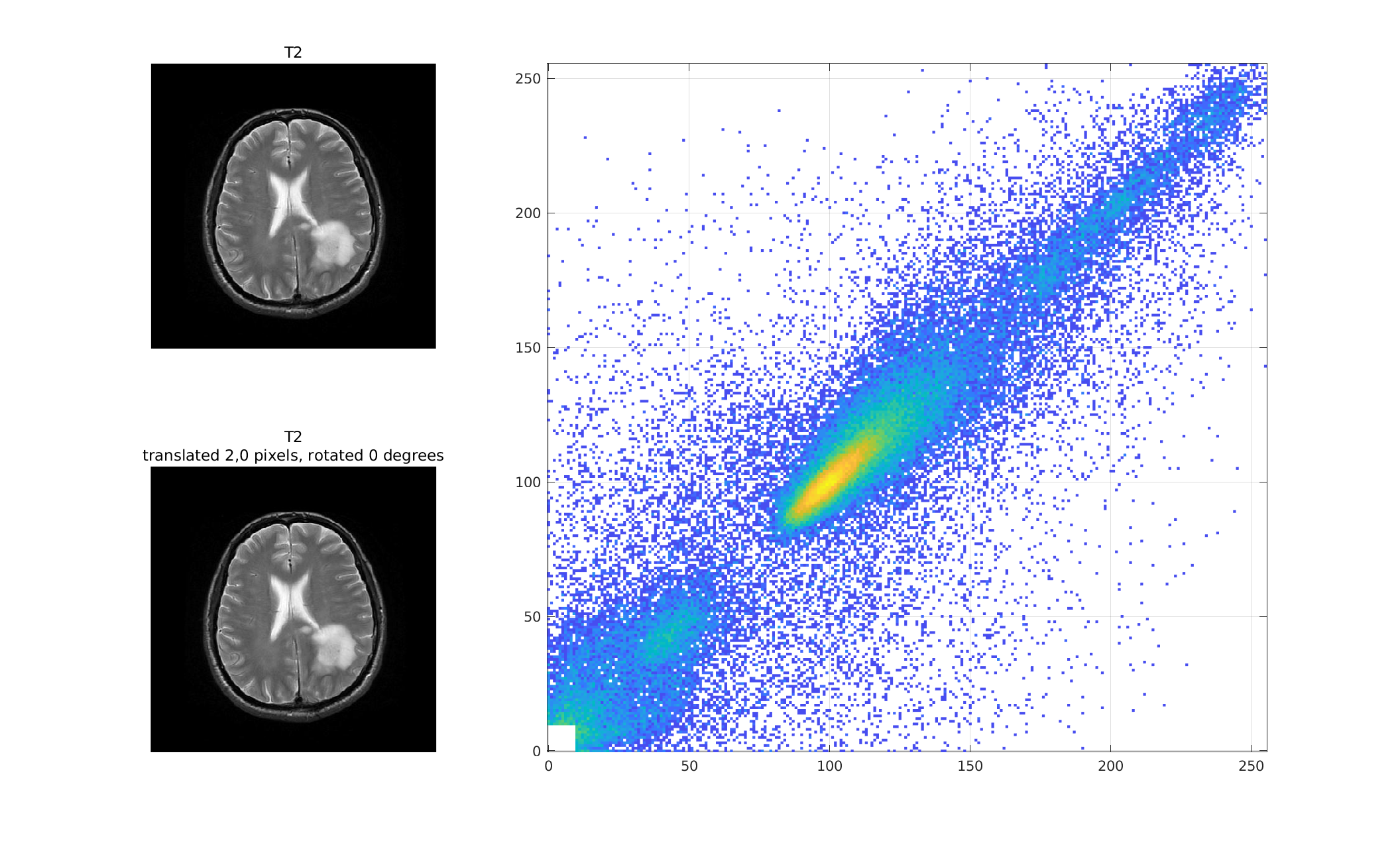
And with further "de-registration":

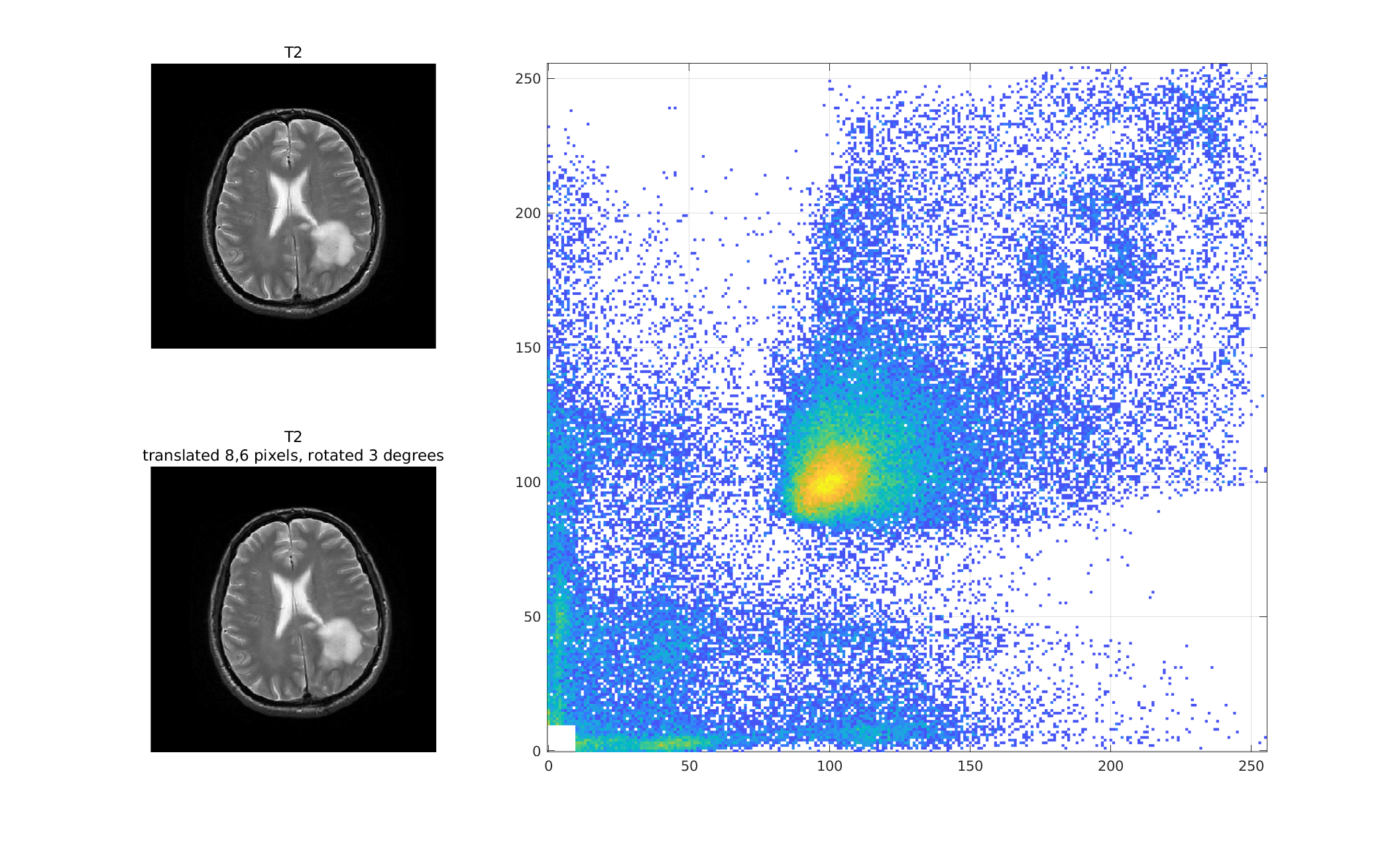
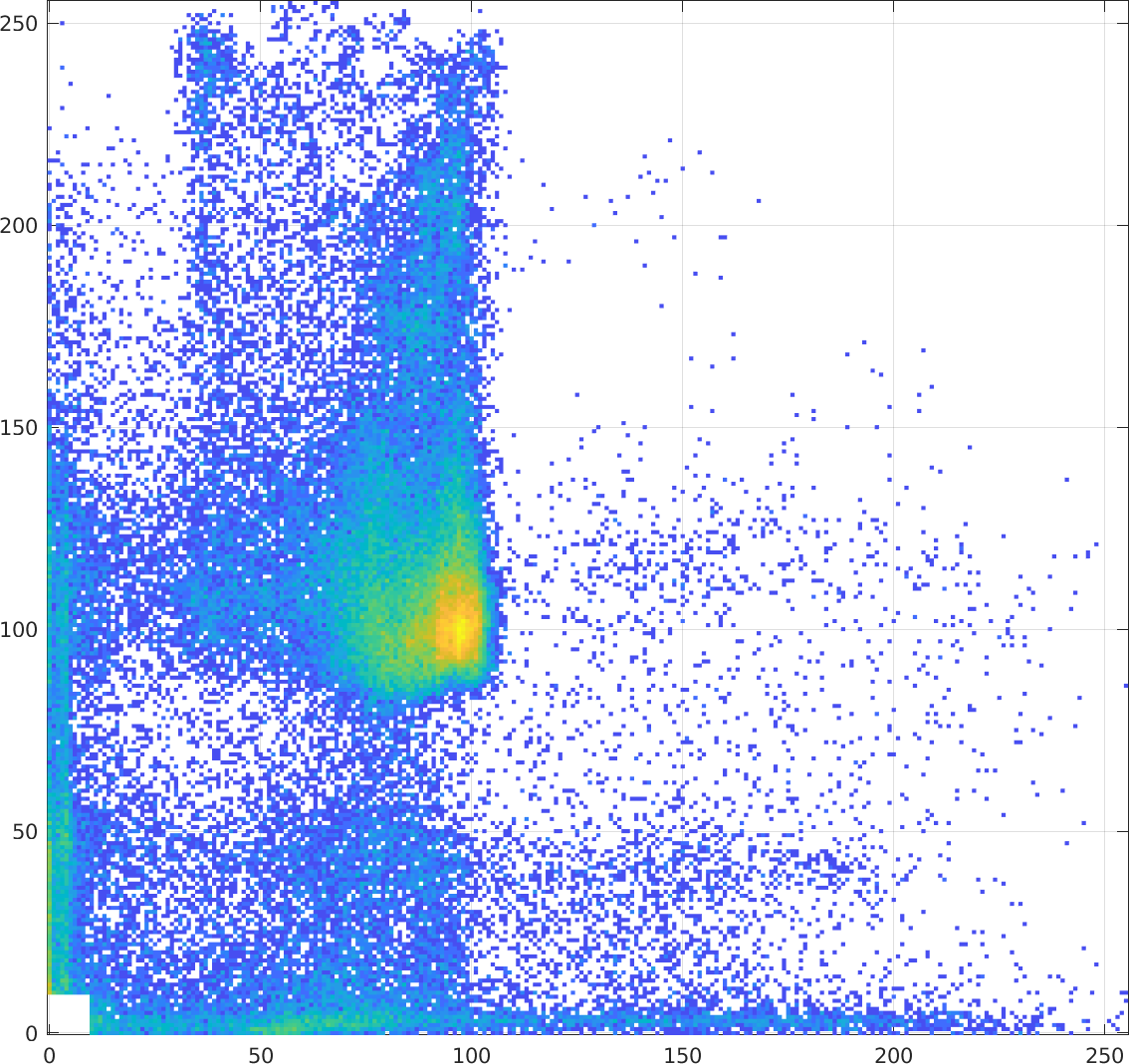
This "diminshed coherence" in the joint histogram holds true even if the images are of different modalities, like the original T1 and T2 images:

$\longrightarrow$ some translation $\longrightarrow$

$\longrightarrow$ some translation and rotation $\longrightarrow$

The entropy of a random variable, $X$, is a measure of the average uncertainty in that variable: If entropy is large, we know less about the next value of the random variable. From the last lecture,

$H = - \sum_k P(k) \log P(k)$

Conditional entropy describes the average uncertainty in a random variable, $X$, given knowledge of another random variable, $Y$.

In terms of pixel intensities, $Y$ is the intensity of a pixel in one image and $X$ is the intensity of the corresponding (overlapped) pixel in the other image. If the images are aligned, $Y$'s value should be a good predictor of $X$'s value. If so, the conditional entropy of $X$, given $Y$, should be low, since there is not much uncertainty in $X$ if we already know $Y$, since $Y$ is a good predictor of $X$.

The conditional entropy of $X$, given $Y$, is

$H(X|Y) = \sum_y P(y) \left[ \; - \sum_x P(x|y) \log P(x|y) \; \right]$

The outer sum is the probability-weighted average value of the thing in the square brackets, taken over all values, $y$, of $Y$.

The thing in the square brackets is the entropy of $X$, given that we know the random variable $Y$ has value $y$. This is just like the entropy of $X$, but takes into account the fact that $y$ is known. Usually, the probability that $X = x$ is denoted $P(x)$; if we know that $Y = y$, then the conditional probability that $X = x$ is denoted $P(x|y)$. The thing inside the square brackets is the entropy of $\mathbf P\mathbf (\mathbf x\mathbf |\mathbf y\mathbf )$.

So conditional entropy, $H(X|Y)$, gives a formal measure of how well knowledge of $Y$ (the intensity of a pixel in one image) can predict $X$ (the pixel intensity of the overlapping pixel in the other image).

$H(X|Y)$ should be minimzed (since it's the entropy) when $Y$ best predicts $X$. For example, if $H(X|Y) = 0$, $Y$ exactly predicts $X$.