A classic problem in computer-assisted surgery is to find the transformation between a set of fiducial markers on the patient in the operating room, and the same set of markers in a computer model.
Example
For example, fiducials can be attached to the head prior to a scan:
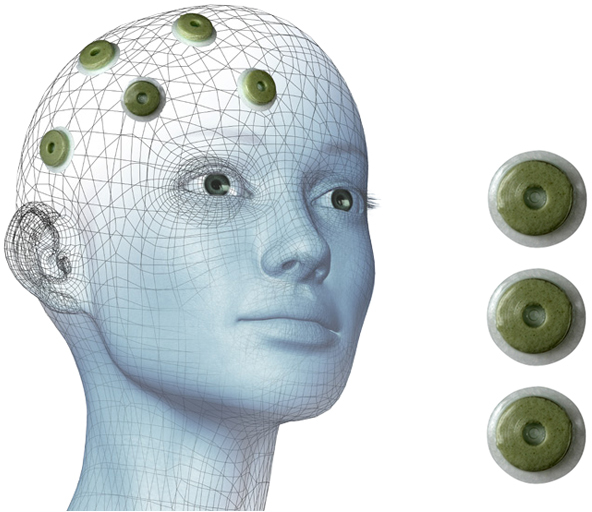[belucomed.com]
The scan permits a 3D computer model of the skull to be made:
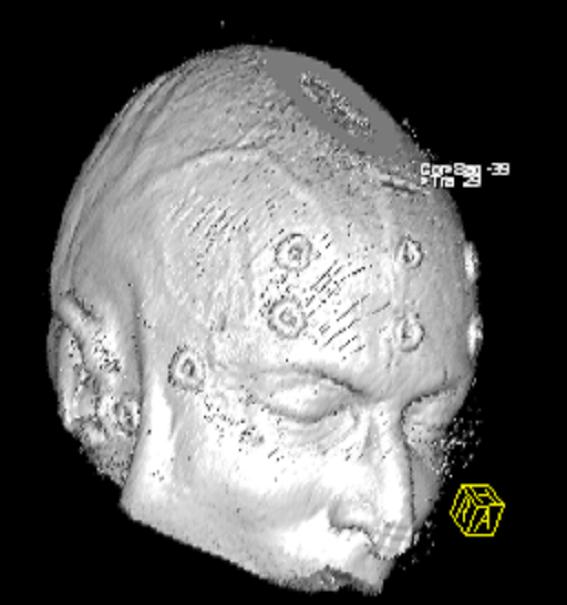[cedars-sinai.edu]
The operation can then be planned on the computer model. Once the patient is in the operating room, the surgeon can use a stylus to find the 3D positions of the fiducials.
Then a transformation is computed between the 3D facial fiducials and the same 3D fiducials in the computer model. This transformation allows the positions of the tracked surgical tools to be shown on the computer model during the operation, so that the surgeon can align the tools with the plan on the computer model.
The Problem
Given two sets of 3D points, $p_1, \; p_2, \ldots, p_n$ and $q_1, \; q_2, \ldots, q_n$ such that $\mathbf p_i$ corresponds to $\mathbf q_i$, find a rotation $R$ and a translation $t$ that maps the $p_i$ onto the $q_i$ with minimal error.
In other words, find $R$ and $t$ that minimize
$\sum_i | (R \; p_i + t) - q_i |$
The problem is called the "orthogonal Procrustes problem" and was first solved by Schönemann in 1964. Other, related solution were presented by Arun, Huang, and Blostein (known as "Arun's method") and by Horn (known as "Horn's method").
Finding $\large \mathbf R$
It can be shown that the error is minimized when the centroids of the two point sets coincide, so we will first modify the points in each set by subtracting that set's centroid: $$\bar{p} = {1 \over n} \sum_i p_i \qquad\textrm{and}\qquad \bar{q} = {1 \over n} \sum_i q_i$$
Let $P = [\ p'_1,\ p'_2,\ \ldots,\ p'_n\ ] \textrm{ where } p'_i = p_i - \bar{p}$.
Let $Q = [\ q'_1,\ q'_2,\ \ldots,\ q'_n\ ] \textrm{ where } q'_i = q_i - \bar{q}$.
We need to find the rotation $R$ that minimizes:
$| R \; P - Q |_F$
Let $U \; \Sigma \; V^T$ be the singular value decomposition of the cross-covariance matrix, $Q\ P^T$.
Then $R = U \; V^T$.
Proofs can be found in Arun, Huang, and Blostein's paper and on Wikipedia.
Finding $\large \mathbf t$
$R$ rotates the centred $p'_i$ to best align with the centred $q'_i$. We must then translate these points back toward the centroid of the original $q_i$ with this operation: $$\begin{array}{rcl} R\ p'_i + \bar{q} &=& R\ (p_i - \bar{p}) + \bar{q} \\ &=& R\ p_i + (\bar{q} - R\ \bar{p}) \\ &=& R\ p_i + t \end{array}$$
So the translation is $t = \bar{q} - R\ \bar{p}$.