In computer-assisted surgery, there are different coordinate systems attached to different objects:
- a world coordinate system is usually fixed to the a "tracker" that is observing everything;
- a tool coordinate system is fixed to a surgical tool (there could be multiple such coordinate systems for multiple tools); and
- a patient coordinate system is fixed to the patient, usually to a bone or rigidly attached frame.
In the operating room below, the world coordinate system is at the centre of the optical tracker with its axes aligned to the principal axes of the optical tracker:
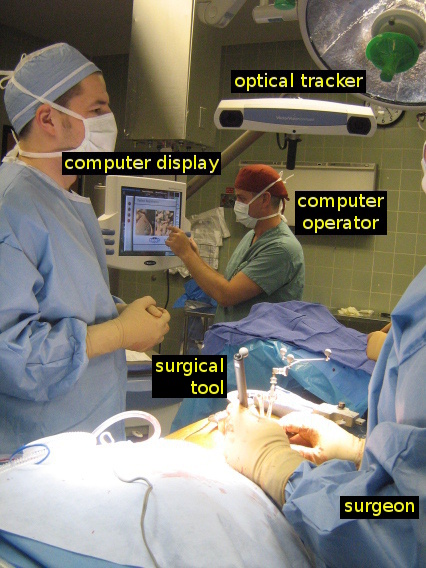
The tool below has a set of reflective spheres attached. The origin of the tool coordinate system is near the centre of the four reflective spheres. These spheres can be seen by the optical tracker and the optical tracker can determine the transformation from the tool coordinate system, TCS, to the world coordinate system, WCS.
The cutting surface of the tool has a position that is defined in the tool's coordinate system.

A common mathematical operation is to transform coordinates between these coordinate systems.
For example, to find where tool's cutting surface is in the world coordinate system, we would have to transform its position from the tool system to the world system.
If $T^A_B$ is the transformation that maps from coordinate system $A$ to coordinate system $B$ and $p_A$ is a position in coordinate system $A$, then $p_B$ is the same position in coordinate system $B$: $$p_B = T^A_B\ p_A$$
(Some books will use the notation $T_A^B$ for this transformation, so be sure that you know which convention is being used.)
Transformation from origin and axes
Transformations in 3D are done using 4D homogeneous coordinates. (For a review, see CISC 454 notes on homogeneous coordinates.) Transformations between coordinate systems can be represented with $4 \times 4$ matrices.
Each coordinate system has an origin and three orthogonal axes.
Suppose we have the tool's origin, $o$, and axes, $u, v, w$, all written as vectors in the world coordinate system, WCS.
The tip of the tool has position $p_t$ in the tool coordinate system.
But we need this to know where the tool tip is in the world. So what is the transformation, $T^t_w$, that transforms $p_t$ into its equivalent position, $p_w$, in the world system? $$p_w = T^t_w\ p_t$$
First, realize that $p_t$ has coordinates $(a,b,c)$ in the TCS. That means that $p_t = a\ u + b\ v + c\ w$ in the WCS, since $u$, $v$, and $w$ are written in the WCS.
As a homogeneous transform, this is $$p' = \left[\begin{matrix} \vdots & \vdots & \vdots & 0 \\ u & v & w & 0 \\ \vdots & \vdots & \vdots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] \ p_t$$
This $p'$ is in the WCS, but it's a vector from the origin of the TCS. So we have to add the origin, $o$, to $p'$ to get $p_w$. (See the vectors in the image above.)
As a homogeneous transform, this is $$p_w = \left[\begin{matrix} 0 & 0 & 0 & \vdots \\ 0 & 0 & 0 & o \\ 0 & 0 & 0 & \vdots \\ 0 & 0 & 0 & 1 \\ \end{matrix}\right] \ p'$$
And the combined transform is $$ p_w = \left[\begin{matrix} 1 & 0 & 0 & \vdots \\ 0 & 1 & 0 & o \\ 0 & 0 & 1 & \vdots \\ 0 & 0 & 0 & 1 \\ \end{matrix}\right] \left[\begin{matrix} \vdots & \vdots & \vdots & 0 \\ u & v & w & 0 \\ \vdots & \vdots & \vdots & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right] p_t$$
or $$ p_w = \underbrace{\left[\begin{matrix} \vdots & \vdots & \vdots & \vdots \\ u & v & w & o \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 1 \end{matrix}\right]}_{T^t_w} p_t$$
Note that $p_t$, as a 4D homogeneous point, has a 1 in its last position.
Inverse transformation
The inverse of this is, $T^w_t$: $$ p_t = \underbrace{\left[\begin{matrix} \cdots & u & \cdots & -o \cdot u \\ \cdots & v & \cdots & -o \cdot v \\ \cdots & w & \cdots & -o \cdot w \\ 0 & 0 & 0 & 1 \end{matrix}\right]}_{T^w_t} p_w$$
This transformation projects $p_w$ onto each of the axes $u, v, w$, then projects $o$ into the TCS and subtracts it.
Chains of Transformations
A common mathematical operation is to find the position of the tool tip in the coordinate system of the patient.
Suppose $T^t_w$ transforms from the tool to the world, while $T^p_w$ transforms from the patient to the world.
Then if $p_t$ is the tool tip in the TCS, what is the tranformation, $T^t_p$, that maps $p_t$ to the equivalent $p_p$ in the patient coordinate system? $$p_p = T^t_p\ p_t$$
Following the arrows above, $$T^t_p = (T^p_w)^{-1}\ T^t_w$$