There is an excellent guide to MRI at mriquestions.com. Most images in these notes come from that site, courtesy of Allen D. Elster, MRIquestions.com.

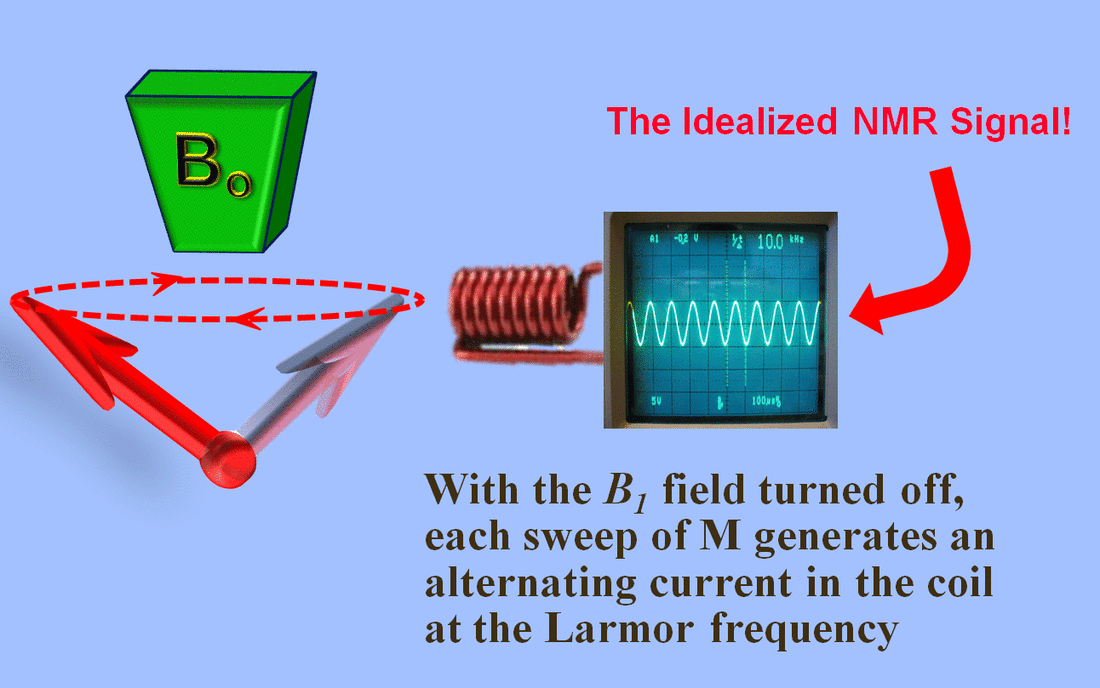
When $B_1$ is turned off, atoms interact with environment and lose energy. Upon energy loss, their magnetic moment re-aligns with $B_0$. This is called relaxation.

The thermal energy loss is tiny in the human body, so no harm comes to the subject.

We can split $M$ into two components: $M_z$ which is aligned with the $B_0$ axis, or the $z$ axis as it is also labelled; and $M_{xy}$ which is perpendicular to $M_z$:

$M = M_z + M_{xy}$

After $B_1$ is turned off, the precession continues with the same (Larmor) frequency and same phase, but the net magnetic moment, $M$, "tilts up" to align with $B_0$.

• The magnitude of $M_z$ increases as $|M_z| = |M_0|\ (1 - e^{-{t \over \textrm{T1}}})$, which we've seen before.
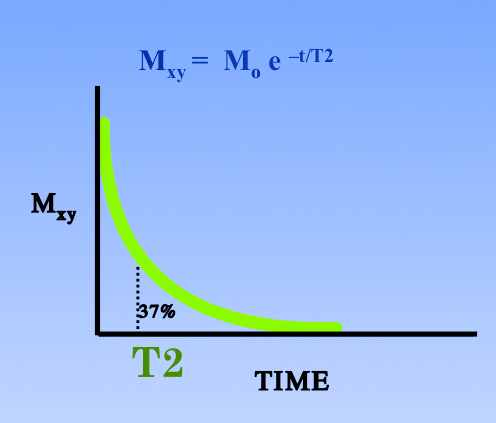
• The magnitude of $M_{xy}$ decreases as $|M_{xy}| = |M_0|\ e^{-{t \over \textrm{T2}}}$, which is new.

As before, T1 is the time that $|M_z|$ takes to reach about 63% of $|M_0|$.

And T2 is the time that $|M_{xy}|$ takes to reach about 37% of $|M_0|$.

This means that T2 is always less than T1:

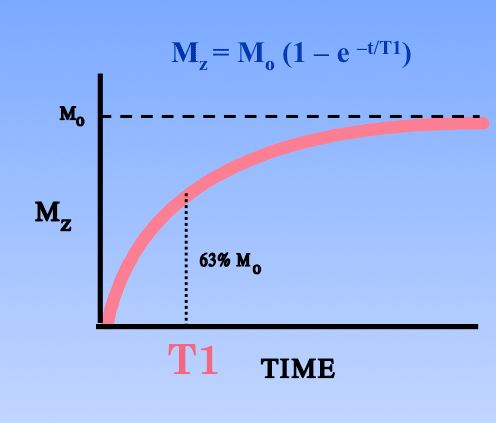
T1 is in [0.1, 3.0]. T1 is the time constant for the net magnetic moment, $M_z$, in the $B_0$ direction.

T2 relaxation occurs from interactions with spins of close particles and local changes in the magnetic field, both of which cause a proton to fall out of phase with the rest of the in-phase protons.

T1 and T2 depend on molecule containing the $^1H$. Small fast molecules have long T1 and T2. Slow molecules get shorter T2 and longer T1:

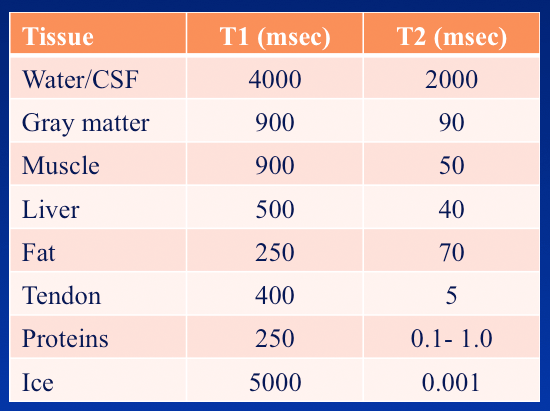
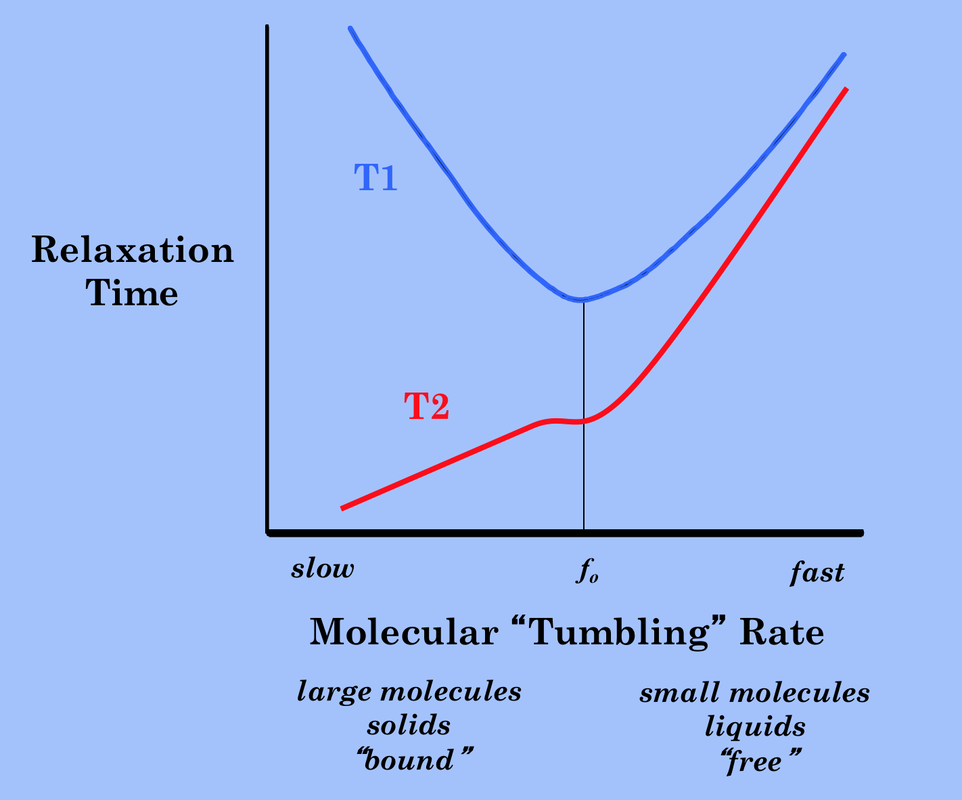
Longitudinal relaxation (T1) induces transverse relatation (T2) because the net spin, as it lines up with $B_0$, gets a smaller component in the transverse direction. But additional factors contribute to transverse relaxation, so it's usually faster (but never slower).

The Faraday-Lenz principle of magnetic induction states that "a voltage (V) is generated in a coil proportional to the rate of change of the magnetic field (dB/dt)".

So the circularly varying $M_{xy}$ (see the $xy$ plane in the figure of $M_z$ and $M_{xy}$ above) is a changing magnetic field and can induce a voltage in a receiver coil.

The received signal is

$\sin \omega\ t$

where $\omega$ is the Larmor frequency, but expressed in radians/second.

This figure shows the received signal if $M_{xy}$ were not to decay:

But $M_{xy}$ does decay with the time constant T2, described above.

In fact, $M_{xy}$ decays faster than T2 due to inhomogeneities in the main field, $B_0$, which result in different precession frequences at different points in the (tiny) volume and dephasing of individual magnetic moments.

This faster rate is denoted T2* and the physical process is called free induction decay or FID.

Then the received signal, incorporating the sinusoidal osciallation and the T2* decay, is

$|M_{xy}| = (\sin \omega \: t) \; e^{-{t \over \textrm{T2*}}}$

and is shown in the figure below:

This is the only signal received in MRI!