There is an excellent guide to MRI at mriquestions.com.
Most images in these notes come from that site, courtesy of Allen D. Elster, MRIquestions.com.
Net magnetic field
The following will consider just the protons of $\mathbf{^1H}$ nuclei
within a very small volume of space, say 2mm x 2mm x 5mm (like a
single voxel in an MR image).
Without a strong magnetic field, the proton axes in this volume
are randomly oriented:

The MRI machine produces a strong magnetic field, $B_0$, which is
typically transverse to the subject's body.
This field causes the protons to align with the field in parallel
or anti-parallel directions:

Under a $B_0$ of 1.5 Tesla, for example, out of 2 million
nuclei, only about 9 more will be parallel to $B_0$ than
anti-parallel. But a 2mm x 2mm x 5mm voxel of water contains
$10^{21}$ nuclei, so about $10^{15}$ more proton are parallel than
antiparallel.
These "excess" protons provide the measurable magnetic field.
Let $M$ equal the sum of all the magnetic moments, which
are the vectors respresenting the individual magnetic fields.
This sum (which is represented as a vector) is the net magnetic
field.
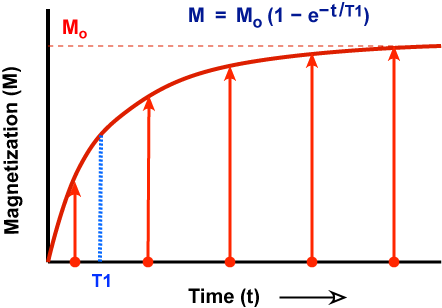
After $B_0$ is turned on, it takes a while for the protons to
line up with $B_0$:
$M(t) = M_0\ (1 - e^{-{t \over \textrm{T1}}})$
where $M_0$ is the final, maximum magnetization and T1 is the time it takes for $M$ to reach 63% of $M_0$:
Magnetic resonance
$M$ is made of of contributions from all the spinning proton.
Each proton spins on a different axis and has its own magnetic
moment. But the sum of these magnetic moments is $M$.
$M$ does not precess after the initial application of
$B_0$, because the individual protons, while precessing, are not
precessing in phase.
When an oscillating magnetic field, $B_1$, is applied
perpendicular to $B_0$ and at the Larmor frequency of the protons,
some of the individual protons will begin to precess in phase with
the oscillating field. So $M$ will begin to precess.
The $B_1$ field must inject energy at the natural (Larmor)
frequency of the system if oscillation (precession) of the system
is to be induced.
Intuition (perhaps misleading)
Consider pushing a child's swing. To add energy to this
system, the pushes have to be timed to match the period of the
swing's oscillation. In other words, the frequency of the
pushes must match the frequency of the system.
Another classic example is the Tacoma Narrows Bridge, where
the frequency of the wind matched the natural frequency of the
bridge structure, so the wind was able to increase the
oscillation of the structure:

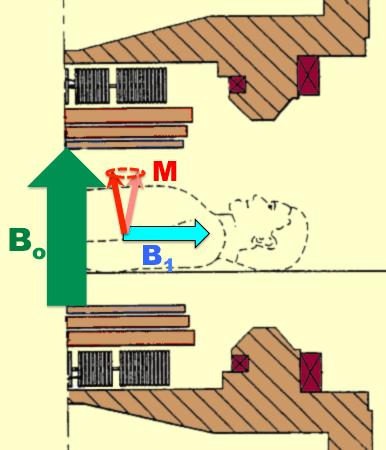
The image below shows a cross-section of an MRI machine with
$B_0$ induced by magnets above and below the patient, and with
$B_1$ induced by a coil of wire (not shown) around the patient.
The net magnetic field, $M$, is precessing:
Magnetic resonance occurs when energy is transferred from
$B_1$ to $M$. The frequency of $B_1$ must be within 3-5% of
the Larmor frequency for this to happen.
Pulses and tip angles
The tip angle, $\alpha$, is the precessional
angle of $M$ with respect to $B_0$.
The tip angle depends on the strength of $B_1$ and the duration,
$\Delta t$, for which $B_1$ is applied:
$\alpha = \gamma \; B_1 \; \Delta t$
Note that a $B_1$ pulse changes the spin of only some
$^1H$ protons, while almost all other protons are unaffected.
But those protons that are affected will have a net
magnetic moment, $M$, that precesses around $B_0$.
A 90 degree pulse is a $B_1$ of a particular field
strength and for a particular duration, $\Delta t$, such that
$\alpha = \gamma \; B_1 \; \Delta t = 90 \textrm{ degrees}$
You can have pulses for any angle.
A 180 degree pulse actually inverts the direction of $M$.
And further energy added by $B_1$ will eventually bring the
direction of $M$ to 360 degrees, or its original orientation.
(This is where our classical intuition starts to break down.)
up to Schedule & Notes


