There is an excellent guide to MRI at mriquestions.com. Most images in these notes come from that site, courtesy of Allen D. Elster, MRIquestions.com.

There are lots of other explanations of MRI on the web. One is Simply Physics (only an introductory chapter 2 is available online)

But the mriquestions.com site seems to be the clearest and most comprehensive.

See also the amazingly excellent Paul Callaghan videos.

Here are some MRI images:

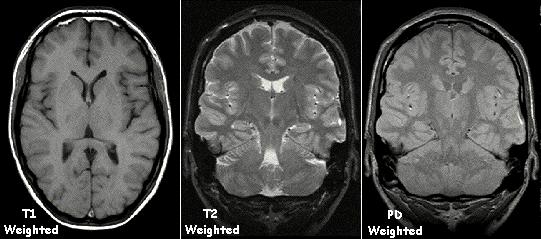
MRI images provide multiple "views" of the anatomy; these are usually the "T1-weighted", "T2-weighted", and "PD-weighted" views, which we'll discuss more in later lectures.

The combination of views, of course, provides more information that a single view. A tissue classification at a pixel can often be made by looking at the three different values of the corresponding pixel in the three views.

MRI works by creating a magnetic field, or fields, across the patient. This causes the nucleus (a proton) of each hydrogen atom in the patient to align with the field. When the field is turned off, these protons eventually return to their original state and, in doing so, emit energy as radiofrequency (RF) waves. The time that these protons take to "de-align" can be determined by analysing these RF signals and used to produce the MR image.

$^1H$ is a hydrogen atom consisting of one proton and one electron.

The proton nucleus has a property called "spin" which has parallels to the property of angular momentum in rotating objects.

In quantum mechanics:

• spin = a (spin up) + b (spin down)
• both exist simultaneously but only one appears when observed
• $|a|^2$ and $|b|^2$ are the probabilities of each being observed

But we usually think of the spin as up or down only. Spin up is parallel to the ambient magnetic field (low energy state). Spin down is anti-parallel to the ambient magentic field (high energy state).

In terms of a $^1H$ proton with "spin", the picture looks like this:

Think of toy top spinning. It has angular momentum around the axis of spin. The gravity field exerts a force downward.

A spin axis that is tilted with respect to the gravity field will result in precession, or a rotation of the spin axis around the direction of the gravity field:

Under a stronger gravity field, the precessional frequency would increase:

The same is true of a $\mathbf{^1H}$ proton spinning in a magnetic field.

The precessional frequency, $f_0$, of the proton is proportional to the strength of the magnetic field, $B_0$.

The relation is described by the Larmor equation:

$f_0 = \gamma\ B_0$

The precessional frequency, $f_0$, is measured in Hz, or "cycles per second". It can also be measured in "radians per second": $w_0 = 2 \pi\ \gamma\ B_0$

The gyromagnetic ratio, $\gamma$, depends upon the size, mass, and spin of the particle (in our case, $^1H$). Some example values of $\gamma$ are:

Particle	Gyromagnetic ratio ($\mathbf\gamma$)
$^1H$	42.58 MHz/Tesla
$^{13}C$	10.71 MHz/Tesla
$e^-$	-27,204 MHz/Tesla

Note that no energy is gained or lost in precession, as the precession angle (between the spin axis and the field direction) remains constant. Energy is required to change the precession angle.

All $^1H$ are precessing under Earth's magnetic field (which is about 50 $\mu T$, or 50 microTesla) at about 2 kHz.