[ Understanding Evolution at evolution.berkeley.edu ]
A subsequence of a string, $s$, is any string, $s'$, that can be made by deleting characters from $s$.
A common subsequence of two strings, $s_1$ and $s_2$, is a string, $s'$, that is a subsequence of both $s_1$ and $s_2$.
For example, a common subsequence of "shoreline" and "helenic" is "heln".
We'll discuss how to use dynamic programming to find the longest common subsequence (LCS) of two strings.
There are many applications of LCS, including:
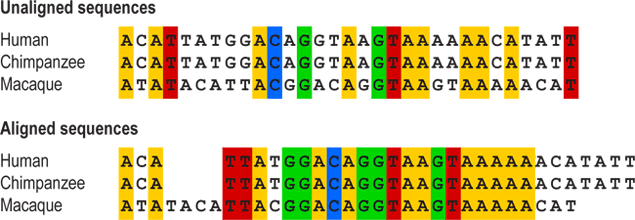
For example, here are three DNA sequences of the same length that appear substantially different when not aligned, but substantially similar when aligned by a long common subsequence. Note that the highlighted subsequence is not the LCS:

[ Understanding Evolution at evolution.berkeley.edu ]
Let $P = p_1\ p_2\ p_3\ \ldots\ p_n$ and $Q = q_1\ q_2\ q_3\ \ldots\ q_m$ be the two strings for which we want to find the LCS.
Let $\LCS(P,Q)$ be the length of the longest common subsequence of $P$ and $Q$.
As with any dyanmic programming problem, we need to define $\mathbf{\mathbf{LCS}(P,Q)}$ in terms of smaller subproblems that can be evaluated recursively.
Let's consider smaller subproblems in which we remove the last character, $p_n$, from $P$ and/or remove the last character, $q_m$, from $Q$.
Then there are four situations:
Otherwise, the last characters are not identical:
For the latter three cases, we don't know which is the maximum, so we have to evaluate all three and pick the maximum.
To simplify the notation, we'll define $$\LCS(i,j) = \LCS( p_1 \ldots p_i, q_1 \ldots q_j ) .$$
Then we have (using $i$ in place of $n$, and $j$ in place of $m$ to indicate that we could be at any prefix of the strings):
if $p_i = q_j$ $$\LCS( i, j ) = 1 + \LCS( i-1, j-1 )$$
else $$\LCS( i, j ) = \max( \ \ \begin{array}[t]{l} \LCS( i-1, j ), \\ \LCS( i, j-1 ), \\ \LCS( i-1, j-1 ) \ \ \ ) \end{array}$$
As this is recursive, we need some base cases, which occur when the string has length zero:
$\LCS(i,0) = 0$
$\LCS(0,j) = 0$
As with the contour joining problem, we can build a table, LCS[i,j], and fill it in, starting from the"smallest" subproblem and going in order of increasing subproblem size.
Subproblem sizes range from $(0,0)$ (the base case) to $(n,m)$, so we need a table of size $(n+1) \times (m+1)$ to store the subproblem results.
Here's a example table for strings $P$ = "mailroom" and $Q$ = "palindrome". Note the $p_0$ column and $q_0$ row for the base cases, which already have their LCS filled in.
To avoid the extra $p_0$ column and $q_0$ row, we could incorporate the base cases as conditional tests in the program code. But this extra row and column allows us to have simpler, cleaner code, so we'll accept the extra memory cost.
As with the contour joining problem, the subproblem size increases left-to-right and top-to-bottom in this table, so we'll fill the table in using that order:
# n = 8
# m = 10
for i=0 to n
LCS[i,0] = 0
for j=1 to m
LCS[0,j] = 0
for i=1 to n
for j=1 to m
if P[i] == Q[j]
LCS[i,j] = 1 + LCS[i-1,j-1]
else
LCS[i,j] = max( LCS[i-1,j], LCS[i,j-1], LCS[i-1,j-1] )
return LCS[n,m]
Note that the code is filling in columns first (in the $j$ loop), then going left-to-right through the columns (in the $i$ loop). It doesn't matter which way it's done, as long as all the smaller subproblems are solved before they are needed.
Here's the result:
To reconstruct the characters of the longest common subsequence, we'll do the same as with the contour joining problem: From cell LCS[n,m] determine which of the three cells, LCS[n-1,m], LCS[n,m-1], and LCS[n-1,m-1], was used to compute LCS[n,m], and go backward to the cell. Then repeat until arriving at a cell with a zero, which means that there's no preceding common subsequence; so we can stop there.
That's not quite everything, as we also have to check for the condition $p_i = q_j$ ...
The resulting backward path is shown here:
Above, the pink cells are those in which $p_i = q_j$ and the character is part of the longest common subsequence. The algorithm "arrives" at those cells from above and left, since the corresponding clause in the code evaluates LCS[i-1,j-1].
In the non-pink cells, the algorithm applies the other clause in the code and evaluates LCS[i-1,j], LCS[i,j-1], and LCS[i-1,j-1], picking the maximum of those. For example, from LCS[6,7], then maximum is to the left, at LCS[5,7].
In the non-pink cells, when there are multiple preceding cells with the same maximum, the algorithm could arrive from any of those. This is the case for the cells above with multiple exiting arrows.
Following any one path will always result in a longest common subsequence of length five. But there could be multiple such subsequences, such as "airom" and "alrom" above, corresponding to the multiple paths.