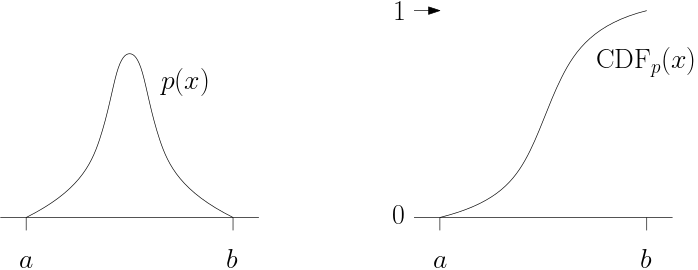
Importance sampling requires that we generate samples according to some nonuniform probability distribution, $p(x)$.
But our code has access to only a uniform random number generator that provides uniform random values in [0,1].
To generate nonuniform random values, we use the Cumulative Distribution Function (CDF).
For a probability density function, $p(x)$, its CDF is $$\textrm{CDF}_p(x) = \int_{-\infty}^x p(u) \; du$$
Recall that a probability density function must integrate to 1 $$\int_{-\infty}^\infty p(x) \; dx = 1$$
So the rightmost, maximum value of the CDF is also 1.
Here's the procedure to generate values $x$ according to $p(x)$:
- Generate $y$ uniformly randomly in [0,1].
- Let $x$ = CDF$^{-1}_p(y)$.
Why this works
In the diagram below, the probability that $y$ is generated randomly in the tiny interval $dy$ is equal to the width of that interval $dy$ divided by the width of the [0,1] interval in which numbers are generated uniformly randomly. So $$P(y \in dy) = dy$$
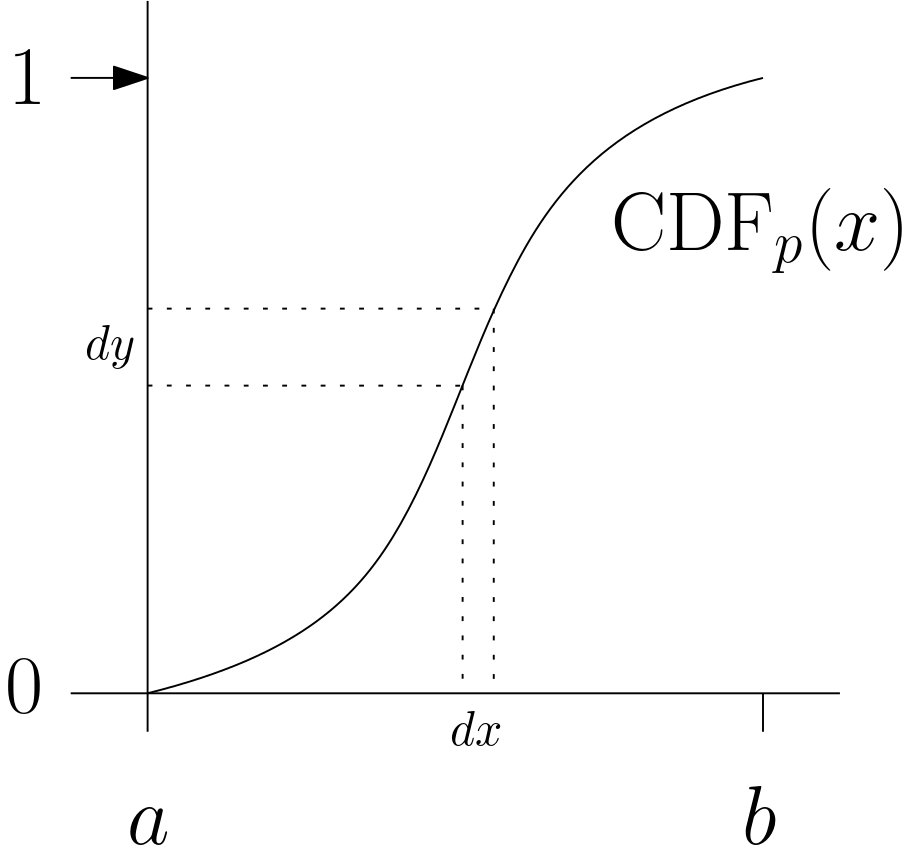
The probability that $x$ is generated randomly in the tiny interval $dx$ is the same as the probability that $y$ is generated in $dy$, since $x = \textrm{CDF}^{-1}_p(y)$. So $$P(x \in dx) = dy$$
But $$\begin{array}{rl} {dy \over dx} &= {d \over dx} \textrm{CDF}_p(x) \\ &= {d \over dx} \int_{-\infty}^x p(u) \; du \\ &= p(x) \textrm{ (by the second fundamental theorem of calculus)} \\ dy &= dx \; p(x) \\ \end{array}$$
So the $P(x \in dx) = dy = dx \; p(x)$, which is exactly the probability distribution that $x$ should have.