Solid Angle
Recall from 2D than the angle subtended by an object, O, from a point, x, is the length of the projection of O onto a unit circle centred at x. It is measured in "unit angles", or radians (rad). The full circle subtends 2 \ \pi radians.
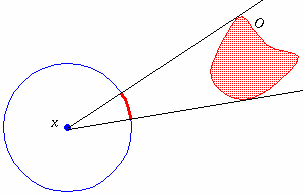
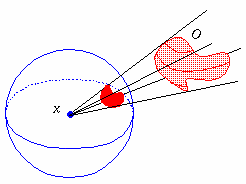
In 3D, the angle subtended by an object, O, from a point, x, is the area of the projection of O onto a unit sphere centred at x. It is measured in "unit solid angles", or steradians (sr). The full sphere subtends 4 \ \pi steradians.
Measures of Illumination
Radiant power (P) is the rate at which light energy is transmitted, and is measured as energy (photons) per unit time, in Watts.
Power at a Point
Flux is the radiant power crossing a particular surface.
Flux density (\Phi) is the radiant power per unit area of the surface, measured in Watts per unit area. At a point, x, surrounded by an infinitesimal surface, dx, the flux density is \Phi(x) = \frac{dP}{dx}.
Incident flux density is the flux density of particles arriving at a surface from all directions. It is also called irradiance (E).
Exitant flux density is the flux density of particles leaving a surface in all directions. It is also called radiosity (B).
Power in a Direction
Consider a point light source. Its radiant intensity (I) is the power radiated per unit solid angle, and is measured in Watts per steradian.
In a particular direction, \omega, surrounded by an infinitesimal solid angle, \domega, the radiant intensity is I(\omega) = \frac{dP}{\domega}.
Power at a Point, in a Direction
Radiance (L) is the flux density at a point, x, in a direction, \omega. Sometimes, the direction is given by two angles: elevation \theta (from the surface normal, n) and azimuth \Phi (from a given direction on the surface).
The flux density is measured with respect to a surface perpendicular to the direction. If the surface at x is not perpendicular to direction \omega, it is projected onto a surface that is.
The figure below shows the radiance at x as the flux density across the surface dx' in the direction \omega:
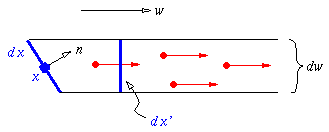L(x,\omega) = \frac{d^2 P}{\domega \ dx'}.
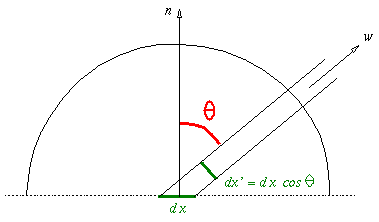
Since the ratio of the areas, dx' and dx, is \cos \theta (where \theta is the angle between \omega and n, the surface normal at x), radiance is typically written as
Radiosity and Radiance
Radiosity is the exitant flux density from a point: B(x) = \frac{d P}{dx}. How does radiosity relate to radiance?
Let \Omega be the set of directions above the surface at x. From the radiance equation above, \begin{array}{rcl} \displaystyle L(x,\omega) &=& \displaystyle \frac{d^2 P}{\domega \ \cos \theta \ dx} \\ \displaystyle L(x,\omega) \cos \theta &=& \displaystyle \frac{d^2 P}{\domega \ dx} \\ \displaystyle{\int_\Omega L(x,\omega) \ \cos \theta \ \domega} &=& \displaystyle{\int_\Omega \frac{d^2 P}{\domega \ dx} \domega} \\ &=& \displaystyle \frac{d P}{dx} \end{array}
Thus
Similarly, for incoming energy, the irradiance is E(x) = \int_\Omega L(x,\omega) \ \cos \theta \ \domega.
Intuitively, the cosine term occurs because the radiance in direction \omega is taken with respect to a surface, dx', perpendicular to the direction, not with respect to the surface itself:
Path Convservation of Radiance
[Sillion & Puech 2.1.2]
Given two points, x and y, the radiance shot from x toward y is equal to that received by y from the direction of x. Radiance is not attenuated with distance.
As a consequence, all we need in order to render an image is the radiance, in the direction of the eye, leaving each point of the scene.
Proof of path conservation
Let dx and d y be infinitesimal areas around x and y. Then the (infinitesimal) power leaving x toward y is d^2 P = L(x,\omega) \ \domega_x \ \cos \Theta_x \ dx.
The power arriving at y from x is equal to that leaving x toward y, since photons are conserved (in the absence of collisions and gravity). Thus d^2 P = L(y,\omega) \ \domega_y \ \cos \Theta_y \ d y.
It remains to show that \domega_x \ \cos \Theta_x \ dx = \domega_y \ \cos \Theta_y \ d y.
Let r be the distance between x and y. Since \domega_x is the angle subtended by dy as seen from x, \domega_x = \frac{d y \ \cos \Theta_y}{r^2}.
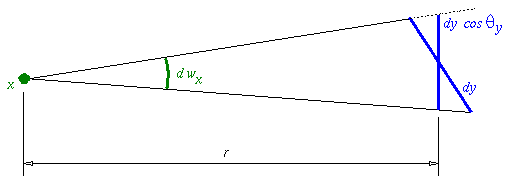
Similary, \domega_y = \frac{dx \ \cos \Theta_x}{r^2}.
And finally, \begin{array}{rcl} \domega_x \ \cos \Theta_x \ dx & = & \frac{d y \ \cos \Theta_y}{r^2} \ \cos \Theta_x \ dx \\ & = & \frac{dx \ \cos \Theta_x}{r^2} \ \cos \Theta_y \ d y \\ & = & \domega_y \ \cos \Theta_y \ d y \end{array}
So L(x,\omega) = L(y,\omega) and radiance is conserved.
Reflection and BRDFs
[Sillion & Puech 2.1.4]
The bidirectional reflectance distribution function at a point, x, is the ratio of the radiance going out in one direction to the flux density coming in from another direction.
Let \omega_i = (\theta_i,\phi_i) and \omega_o = (\theta_o,\phi_o) be the incoming and outgoing directions, respectively.
The incoming directional flux density, d \ \Phi_i, is the flux density of energy arriving from an infinitesimal solid angle, \domega_i, around \omega_i. From the radiance equation, \begin{array}{rcl} \displaystyle{\frac{d^2 P}{dx}} &=& L(x,\omega) \ \cos \theta \ \domega \\ &=& d \ \Phi. \end{array}
The infinitesimal flux density, d \ \Phi, is taken with respect the the infinitesimal solid angle, \domega. The BRDF is then \begin{array}{rcl} \rho_{BD}(\omega_o,\omega_i) &=& \displaystyle{\frac{L_o(x,\omega_o)}{d \ \Phi_i}} \\ &=& \displaystyle{\frac{L_o(x,\omega_o)}{L_i(x,\omega_i) \ \cos \theta_i \ \domega_i}}. \end{array}
Note that the units of the BRDF are per steradian. The reflected radiance due to radiance incoming from a particular direction is L_o(x,\omega_o) = \rho_{BD}(\omega_o,\omega_i) \ L_i(x,\omega_i) \ \cos \theta_i \ \domega_i.
BRDFs and Lambertian Surfaces
A Lambertian surface, or "ideal diffuse surface", has a constant BRDF: \rho_{BD}(\omega_o,\omega_i) = \rho_{BD}.
The radiance of such a surface is independent of direction. The total outgoing radiance in a particular direction, \omega_o, is the integral of reflected radiance from all incoming directions, \Omega: \begin{array}{rcl} L(x,\omega_o) &=& \displaystyle{ \int_{\Omega} \rho_{BD}(\omega_o,\omega_i) \ L_i(x,\omega_i) \ \cos \theta_i \ \domega_i } \\ &=& \displaystyle{ \rho_{BD} \ \int_{\Omega} L_i(x,\omega_i) \ \cos \theta_i \ \domega_i } \\ &=& \rho_{BD} \ E(x) & \text{(recall irradiance, E(x)).} \end{array}
How are radiosity and irradiance related for a Lambertian surface? \begin{array}{rcl} B(x) &=& \displaystyle{ \int_{\Omega} L_o(x,\omega) \ \cos \theta \ \domega } \\ &=& \displaystyle{ \int_{\Omega} \rho_{BD} \ E(x) \ \cos \theta \ \domega } \\ &=& \displaystyle{ \rho_{BD} \ E(x) \ \int_{\Omega} \cos \theta \ \domega } \\ &=& \displaystyle{ \rho_{BD} \ E(x) \ \pi } \\ \end{array}
Inuitively, the quantity \rho_{BD} \ \pi is the fraction of irradiance, E(x), that is reflected (as radiosity, B(x)). This quantity is known as the albedo (\rho): \rho = \pi \ \rho_{BD}.
Then
How are radiosity and outgoing radiance related for a Lambertian surface? \begin{array}{rcl} B(x) &=& \rho \ E(x) \\ &=& \rho \ \left( \frac{L(x,\omega_o)}{\rho_{BD}} \right) \\ &=& \pi \ L(x,\omega_o). \end{array}