Arithmetic encoding codes the entire stream of symbols as a single floating point number.
This method is optimal as the signal size gets very large.
As with Huffman Coding, this method assumes that the probability distribution of the tokens is known and that tokens are independent. This method is used in the Symbol Coder section of the image encoder.
The idea is to split the range [ 0, 1 ] into intervals with:
- one interval for each symbol; and
- the width of an interval being proportional to the symbols' probability.
For example, consider four symbols having these probabilities:
| Symbol | Probability | Interval of [0,1] |
|---|---|---|
| $a_1$ | 0.2 | [ 0.0, 0.2 ] |
| $a_2$ | 0.2 | [ 0.2, 0.4 ] |
| $a_3$ | 0.4 | [ 0.4, 0.8 ] |
| $a_4$ | 0.2 | [ 0.8, 1.0 ] |
The algorithm is
I = [0,1)
for i=1 to n # for n symbols x1, x2, ..., xn
Divide I into intervals of width proportional to symbol probabilities
Narrow I to the interval corresponding to the i^{th} symbol, xi
Output any floating point number in I
Here's how I gets narrower and narrower with successive symbols in the stream $a_1, a_2, a_3, a_3, a_4$:
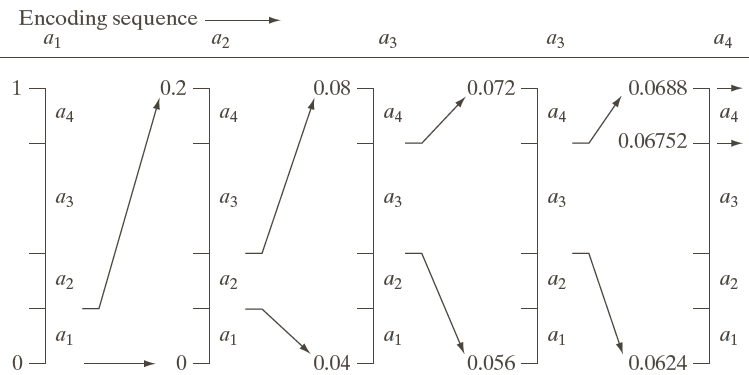
[ G&W figure 8.12 ]
After symbol $a_4$, I is [ 0.06752, 0.0688 ) and any floating point number in that interval can be used to represent the stream of five symbols. We would pick the number that has the shortest representation. If using base-10 digits, for example, we would pick 0.068. But binary encodings are more efficient.
Arithmetic encoding can achieve a bit rate (i.e. bits per symbol) arbitrarily close to the entropy, $H$, of the symbol stream for long streams. This isn't possible with Huffman encoding because of Huffman's constraint that each symbol be encoded separately, so "fractional bits" are wasted with each Huffman-encoded symbol (unless the probabilities are powers of two, in which case there are no fractional bits and Huffman achieves a bit rate of $H$).