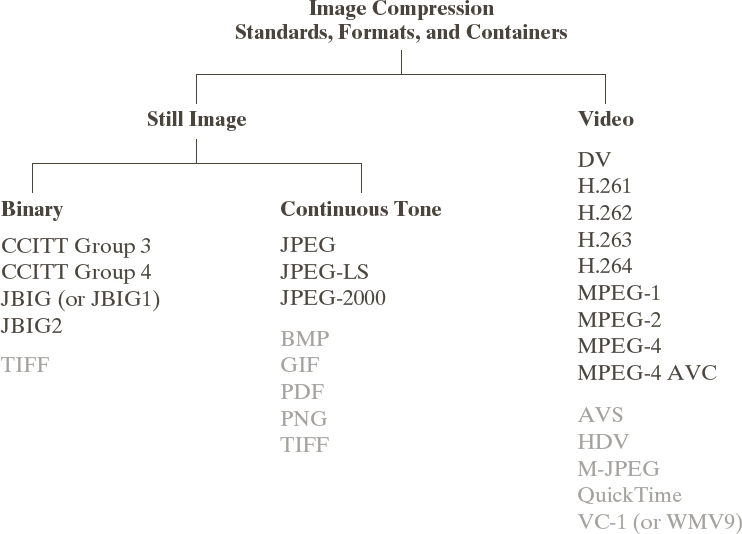
Image and video compression is necessary for storage and
transmission. Consider that a raw standard definition
(SD) video is $720 \times 480$ pixels per frame, with three
bytes per pixel and 30 frames per second. A 90 minute video
would take 156.5 GB if not compressed.
There are several sources of redundancy in an image, which
can be exploited to compress the image.
Coding Redundancy
Here there are only four intensities, but eight bits per pixel:
[ G&W figure 8.1 ]
Let $P(k)$ = probability of value $k$ appearing in the pixel stream.
Then $P(k) = {N_k \over N}$ for $N_k$ the number of pixels of value $k$ and $N$ the total number of pixels.
Let $\ell(k)$ = number of bits to encode value $k$.
Then the average bits per pixel (or "bpp") is
$$L_\textrm{avg} = \sum_k P(k)\ \ell(k)$$
"Variable length encoding" can use different numbers of
bits for different values, and can reduce
$L_\textrm{avg}$. The image above has these pixel values:
| Pixel value |
Probability |
8-bit encoding |
Variable-length
encoding |
| 87 | 0.25 | 01010111 | 01 |
| 128 | 0.47 | 10000000 | 1 |
| 186 | 0.25 | 11000100 | 000 |
| 255 | 0.03 | 11111111 | 001 |
With the variable-length encoding above, the average
pixel requires 1.81 bits, instead of eight bits with the
fixed-length encoding. This is better, even, than a
fixed-length encoding that uses two bits per pixel for
the four different pixel values.
Spatial and Temporal Redundancy
Here, the values on each row are the same and do not need to be repeated:
[ G&W figure 8.1 ]
The rows above can be "run length encoded", where
sequences of the same pixel value can be encoded as a
count, $n$, and a value, $v$, indicating that the next $n$
pixels have value $v$.
Perceptual Redundancy
Here, there are imperceptible differences among the multiple pixel values:
[ G&W figure 8.1 ]
All pixel values could be encoded as a single value
without any perceptible change. But this shouldn't be
done in certain applications, such as medical imaging
where subtle pixel differences might be important.
The process of encoding and decoding an image, $f(x,y)$, is
$$f(x,y) \longrightarrow \fbox{encode} \longrightarrow \textrm{intermediate representation} \longrightarrow \fbox{decode} \longrightarrow f'(x,y)$$
where the "encode" and "decode" operations usually perform
compression and decompression, respectively.
The error incurrred by this process is $e(x,y) = f'(x,y) - f(x,y)$.
Overall error is sometimes represented with the root-mean-square error (or RMS error):
$$e_\textrm{rms} = \left( {1 \over N} \sum_{(x,y)} (f'(x,y) - f(x,y))^2 \right)^{0.5}$$
RMS error is only loosely related to perceptual difference.
For example, here are three different compressions of a figure
from the previous notes, along with their RMS error:
[ G&W figure 8.4 ]
The RMS error is least in the leftmost image,
but greatest in the middle image, even though the
rightmost image appears to have significan missing parts.
An alternative measures is the RMS signal-to-noise ratio:
$$\textrm{SNR}_\textrm{rms} = { \sum f(x,y)^2 \over \sum (f'(x,y) - f(x,y))^2 }$$
Here is the typical encoder/decoder pipeline:
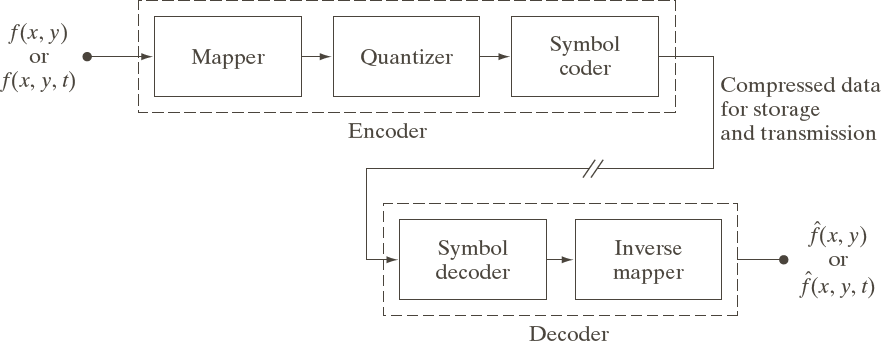[ G&W figure 8.5 ]
In the encoder:
- the mapper tries to reduce redundancy, for example with run-length encoding;
- the quantizer reduces information content, for example by removing low-order bits; and
- the symbol coder generates a stream of symbols, for example by replacing fixed-length symbols with variable-length symbols.
In the decoder:
- the symbol decoder interprets the stream of symbols and
- the inverse mapper undoes the effect of the mapper.
Note that information is lost in the quantizer and is never regained upon decoding!
The combination of an encoder and a decoder is called a codec.
