The Hough Transform can also be used to find circles.
While a line has two parameters ($\theta$ and $r$ in the previous discussion), a circle has three: $$r^2 = (x-a)^2 + (y-b)^2$$
where $(a,b)$ is the circle's centre and $r$ is its radius.
This requires a three dimensional parameter space: $\langle a, b, r \rangle$.
The Hough transform lets each edge pixel vote for all the circles that it might lie on. An edge pixel at $(x_i,y_i)$ will vote for all points, $(a,b,r)$, in the parameter space that satisfy $r^2 = (x_i-a)^2 + (y_i-b)^2$.
For the lines in the previous discussion, each edge pixel voted for points on a sinusoid in the parameter space.
So ... what is the shape of the points voted for in the $\langle a, b, r \rangle$ parameter space?
For a fixed $r = \widehat{r}$, the shape $\widehat{r}^2 = (x_i-a)^2 + (y_i-b)^2$ consists of points $(a,b,\widehat{r})$ that lie on a circle of radius $\widehat{r}$, centred at $(x_i,y_i,\widehat{r})$ and lying in the $r = \widehat{r}$ plane.
A number of those circles of fixed $\widehat{r}$ are shown below:
So an edge pixel $(x_i,y_i)$ votes for all $(a,b,r)$ on the surface of the cone shown above.
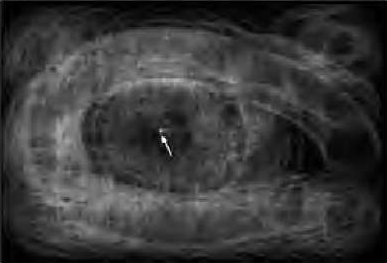
As with the lines, we have to discretize the $\langle a, b, r \rangle$ space into bins and add a vote to each bin that the cone intersects. We usually only look at a small range of $r$ values, so as to reduce the number bins required.
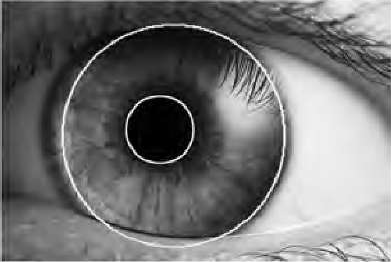
The bins, $(a_i,b_i,r_i)$, with the largest numbers of votes will be those corresponding to circles $r_i^2 = (x-a_i)^2 + (y-b_i)^2$ that were detected in the image.
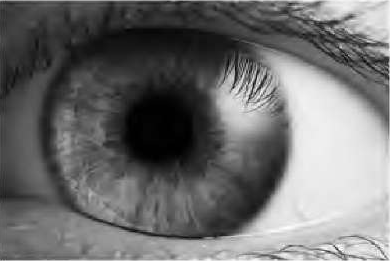
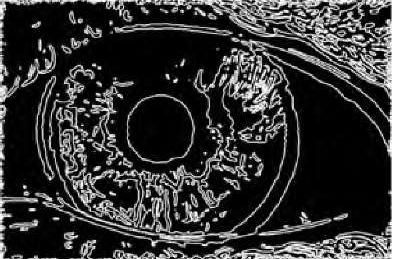
Here's an example of the automatic detection of circles in an image of an eye:
| Original image of eye | Edge pixels from Canny | One 2D slice of 3D accumulator array | Detected circles |
|---|---|---|---|
 |
 |
 |
 |