Periodic Noise Removal
Periodic noise shows up in the frequency domain as high-magnitude coefficients that are distant from the origin. Those coefficients can be edited to zero in the frequency domain, after which the inverse Fourier transform generates the "de-noised" image.
Below, the clown image has low-frequency periodic noise moving in waves from upper-left to lower-right. That corresponds to the two bright spots in the frequency domain, closer to the origin.
There is also a more subtle, higher frequency noise moving in waves from lower-left to upper-right, corresponding to the two bright spots in the frequency domain farther from the origin.
By supressing those spots (i.e. setting them and the region around them to zero), the noise is removed:
 |
FT $\longrightarrow$ |
 |
$\Bigg\downarrow$ Edit |
||
 |
Inverse FT $\longleftarrow$ |
 |
Here's another example. Notice that removal of much of the high-frequency content (i.e. parts farther from the origin in the frequency domain) causes some blurriness:
 |
FT $\longrightarrow$ |
 |
$\Bigg\downarrow$ Edit |
||
 |
Inverse FT $\longleftarrow$ |
 |
Signal Analysis
Machinery Faults
In diagnosing machinery faults, there are usually a lot of rotating parts that cause periodic vibration, or sound. A Fourier Transform of the vibration (from an accelerometer, for example) or sound can tell you what the dominant frequencies are. From the frequency, you might be able to determine what rotating part is causing a problem.
Here is the sound of a vacuum cleaner that has an annoying whine. The Fourier Transform shows a peak around 5445 Hz, which corresponds to a rotating fan blade.
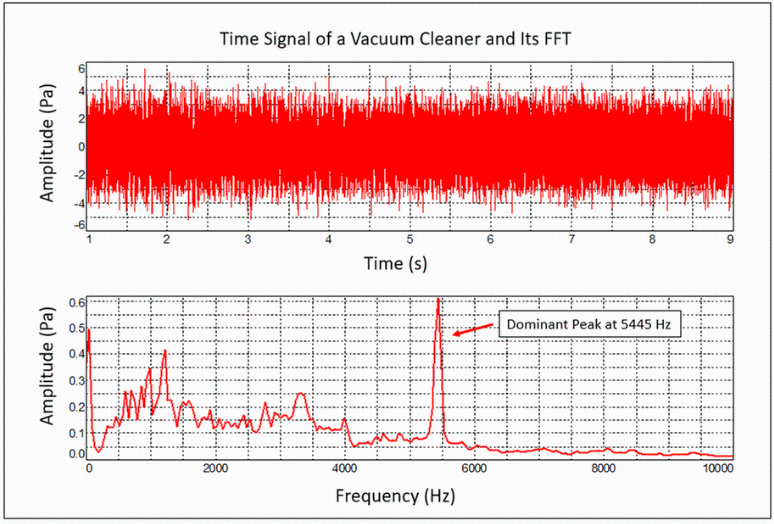
[ from http://community.sw.siemens.com/s/article/what-is-the-fourier-transform]
Vital Sign Measurement
The Fourier Transform can detect heart rate and respiration rate from a photoplethysmogram (PPG), which measures blood volume changes based on light absorption. The blood volume is affected by both the cardiac cycle and the respiratory cycle.
Here's a PPG output for a rat:
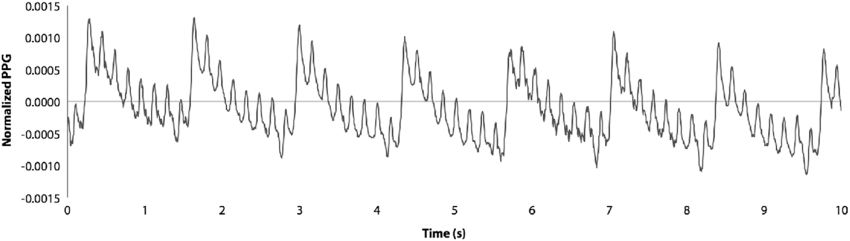
And here's the Fourier Transform showing the respiration rate (about 45 breaths per minute) and the cardiac rate (about 320 beats per minute).
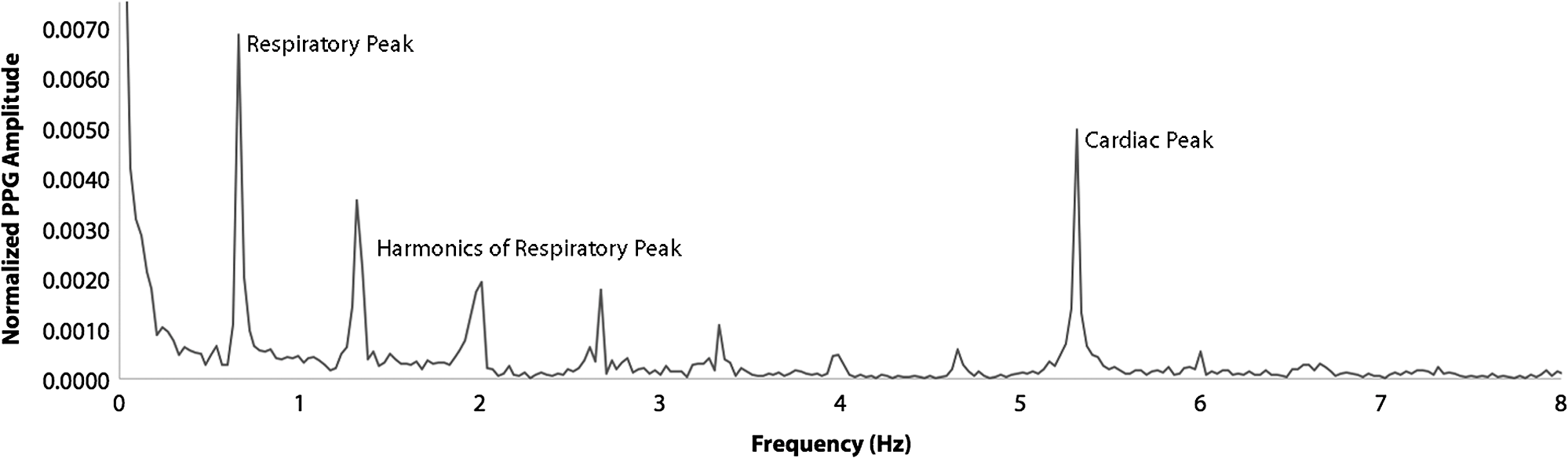
Both images are from "Perfusion assessment in rat spinal cord tissue using photoplethysmography and laser Doppler flux measurements" by J P Phillips, V Cibert-Goton R Langford, and P J Shortland.
Aliasing Example
This is the Fourier Transform of an electrocardiogram (ECG) signal. You can see a spike at 50 Hz, which corresponds to the mains electrical frequency (which is 50 Hz in Europe and much of Asia, but 60 Hz in North America):
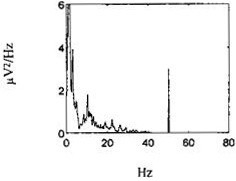
If this had been sampled at 80 Hz, the Nyquist limit would be half that (40 Hz) and all component frequencies would be reflected around the 40 Hz boundary, leading to a spurious 30 Hz signal:
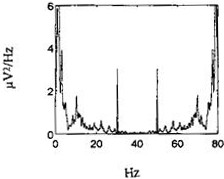
So you should always sample at more than twice the maximum frequency expected to be present in the signal.
Filter Design
Smoothing Filters
Smoothing filters remove high-frequency components in the signal. In 2D, these are the components of the frequency domain that are far from the origin. So a smoothing filter should diminish the magnitudes of of those components, like this:
 |
FT $\longrightarrow$ |
 |
$\Bigg\downarrow$ Edit |
||
 |
Inverse FT $\longleftarrow$ |
 |
Edge Detection Filters
An edge detection filter find high-frequency changes in the image. So components of the frequency domain that are far from the origin should be preserved, while components close to the origin should be suppressed:
 |
FT $\longrightarrow$ |
 |
$\Bigg\downarrow$ Edit |
||
 |
Inverse FT $\longleftarrow$ |
 |
Notch Filters
A "notch filter" will preserve or suppress a certain band of frequencies. This would be useful in removing the 50 Hz signal from the ECG in the example above.
We've left out a huge amount of interesting material about filter design, including box filters, Butterworth filters, and Gaussian filters.
CT Reconstruction
The Fourier Transform is used in CT reconstruction, which is the computing of the internal structure of an object from multiple x-ray images taken around the object. We won't discuss this in this version of the course, but if you're interested you can look at the extra notes on CT reconstruction at the bottom of the Schedule & Notes page.