Let $f$ be a continuous signal with fundamental period $n$.
The continuous signal $f$ can be sampled by multiplying it by an impulse train, $s_T$, with period $T$: $$f \times s_T$$
Also recall that multiplication in the spatial domain corresponds to convolution in the frequency domain: $$\displaystyle \mathscr{F}( f \times s_T ) = \mathscr{F}(f) \ast \mathscr{F}(s_T) = F \ast S_T$$
What does $\mathbf{\mathscr{F}(s_T) = S_T}$ look like?
What does the frequency-domain $S_T$ look like?
Let $\omega_0 = {2 \pi \over T}$. Note that $T$ is the fundamental period of $s_T$.
As discussed previously in the Fourier Transform in 1D, $\omega_0$ is the fundamental angular frequency of $s_T$, which is like the frequency (measured in cycles/unit), but is instead measured in radians per unit, where one cycle is $2 \pi$ radians.
Then $s_T$ can be written as a complex Fourier series:
$ s_T(t) = \sum_k c_k\ e^{ i k \omega_0 t} $
Note that the wavenumber $k$, above, is measured in "cycles per $2 \pi$" and $\omega_0$ is ${ 2 \pi \over T }$, so $k \: \omega_0$ is "cycles per $T$". So $k \: \omega_0$ gives $k$ cycles over the fundamental period and $k$ is what we usually think of as the wavenumber, but for a fundamental period of $T$.
To get the $c_k$, we project as usual onto the Fourier basis functions:
$\begin{array}{rcl} c_k & = & \displaystyle {1 \over T} \int_{-T/2}^{T/2} s_T(t)\ e^{-i k \omega_0 t}\ dt \\ & = & \displaystyle {1 \over T} \int_{-T/2}^{T/2} \left( \sum_j \delta(t - j T) \right)\ e^{-i k \omega_0 t}\ dt \\ & = & \displaystyle {1 \over T} \int_{-T/2}^{T/2} \delta(t)\ e^{-i k \omega_0 t}\ dt & {\rm since\ for}\ t \in [-\frac{T}{2},\frac{T}{2}],\ \delta(t - j T) \neq 0\ {\rm only\ when}\ j=0. \\ & = & \displaystyle {1 \over T} & {\rm since}\ \delta(t) \neq 0\ {\rm only\ when}\ t=0.\ \ {\rm Then}\ e^{i k \omega_0 t} = 1\ {\rm and}\ \int \delta(t)\ dt = 1. \\ \end{array}$
(Above, we can integrate over $[{-T \over 2},{T \over 2}]$ instead of $[0,T]$ because $s_T$ is $T$-periodic.)
Since $T$ is the fundamental period of $s_T$, the frequencies present in $s_T$ are $$\cdots, \frac{-3}T, \frac{-2}T, \frac{-1}T, \frac0T, \frac1T, \frac2T, \frac3T, \cdots$$
and, in the frequency domain, the corresponding $S_T$ looks like this:
where the impulses are the $c_k$ derived above.
Note that $c_k = {1 \over T} + 0 i$.
What does this decomposition of $\mathbf{s_T(t)}$ look like in the spatial domain?
$\begin{array}{rcll} s_T(t) & = & \displaystyle \sum_k c_k\ e^{i k \omega_0 t} \\ & = & \displaystyle a_0 + \sum_{k \geq 1} a_k \cos k \omega_0 t + i\ b_k \sin k \omega_0 t \\ & = & \displaystyle a_0 + \sum_{k \geq 1} \frac2T \cos k \omega_0 t + 0 \sin k \omega_0 t & {\rm since}\ a_k = 2\ \textrm{real}(c_k)\ {\rm and}\ b_k = - 2\ \textrm{imag}(c_k) \\ & = & \displaystyle \frac1T + \frac2T \sum_{k \geq 1} \cos k \omega_0 t \\ \end{array}$
$s_T(t)$ is shown below for $T = 2 \pi$. As the number of terms, $k$, increases, this approaches the periodic delta function of $s_T(t)$.
| 20 terms | 40 terms | 80 terms |
|---|---|---|
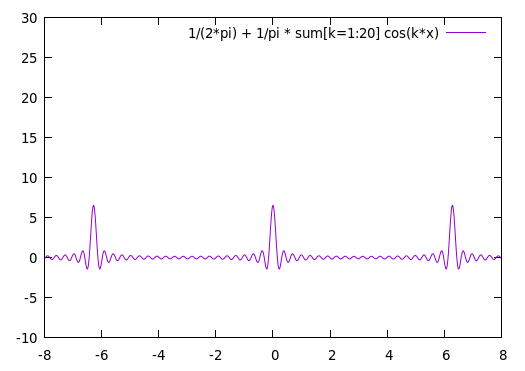 |
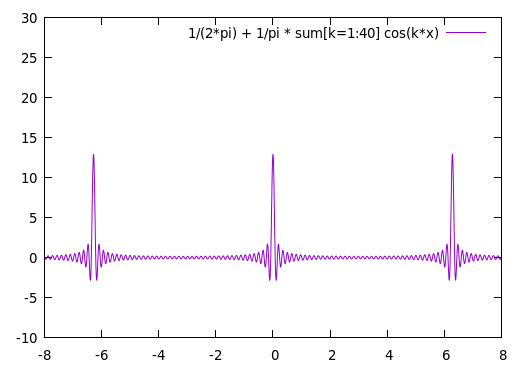 |
 |
What does $\mathbf{\mathscr{F}(f \times s_T) = \mathscr{F}(f) \ast \mathscr{F}(s_T) = F \ast S_T}$ look like?
If $F \ast \delta(\omega_0 - \frac{1}{T})$ is
Then $\displaystyle F \ast S_T = F \ast \sum_j \frac1T \; \delta(\omega_0 - \frac{j}{T})$ is
Box filter $F \ast S_T$
$F \ast S_T$ is periodic with period ${\frac{1}{T}}$, so all of the information lies in $[ \frac{-1}{2T}, \frac{1}{2T} ]$.
So we can multiply $F \ast S_T$ with a "box filter" $B_T$ to remove the extraneous information:
We have lost information where the copies of $F$ overlap.