The fundamental period of a signal is the smallest period over which the entire signal repeats. In other words, it's the smallest $T_0$ such that $f(t + T_0) = f(t)$ for all $t$.
The fundamental frequency is $\omega_0 = {1 \over T_0}$. For a signal that contains multiple frequencies, $\omega_1, \omega_2, \ldots, \omega_N$, the fundamental frequency $\omega_0$ is the highest frequency shared by all of the multiple frequencies. In other words, it's the greatest common factor of $\omega_1, \omega_2, \ldots, \omega_N$.
Note that the fundamental frequency is the highest frequency shared by the constituent frequencies. It's not the highest frequency that is present.
All frequencies present in the signal are an integer multiple of the fundamental frequency.
The fundamental wavenumber is $k_0 = 2 \pi \omega_0 = {2 \pi \over T_0}$.
Example
The plot below shows a signal containing frequencies of $6 \over 2 \pi$ Hz and $15 \over 2 \pi$ Hz, corresponding to wavenumbers 6 and 15. The fundamental frequency of the signal is the greatest common factor these: $\omega_0 = {3 \over 2\pi}$ Hz. The fundamental period is $T_0 = \frac23 \pi$. You can see that the signal repeats every $\frac23 \pi$ units on the $x$ axis.
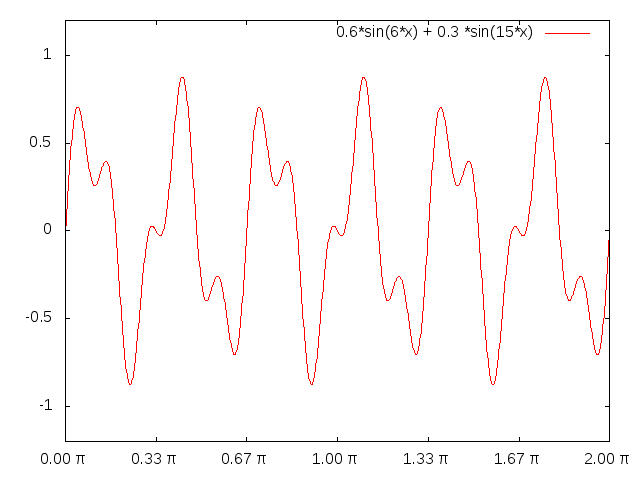
Note that each frequency in the signal is an integer multiple of $\omega_0$: ${6 \over 2 \pi} = 2\ \omega_0$ and ${15 \over 2 \pi} = 5\ \omega_0$.