We're starting on frequency-domain image processing using the Fourier Transform.

forward transform: $\displaystyle F(k) = {1 \over 2 \pi} \int f(x)\ e^{-i k x}\ dx$

inverse transform: $\displaystyle f(x) = \int F(k)\ e^{i k x}\ dk$

From en.wikipedia.org/wiki/Fourier_transform:

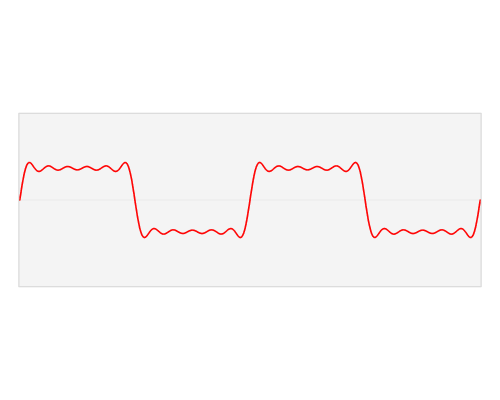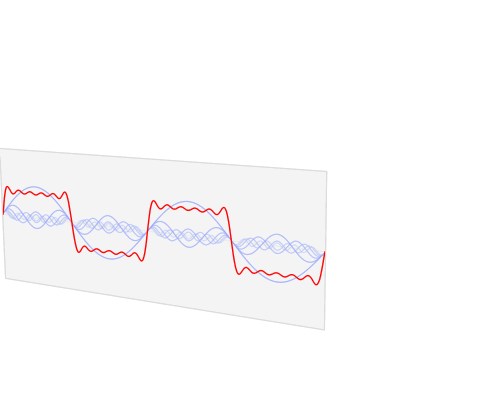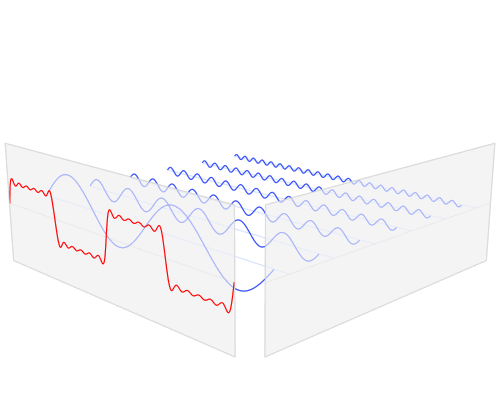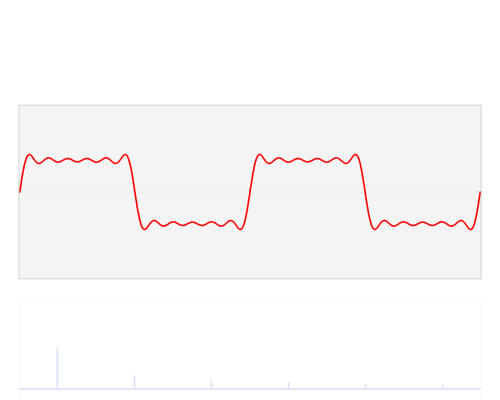
The Fourier Transform maps a signal $f$ in the "spatial domain" (or "time domain" for some people) onto another signal $F$ in the "frequency domain".

In the animation above, what we call $F$ is shown as $\hat{f}$.

In the frequency domain, $F$ shows the sinusoidal waves that are present in the signal $f$, and which sum up to the signal $f$ in the spatial domain.

The animation above shows only the amplitudes of the sinusoidal waves; each wave also has a phase, which is not shown above.

The Inverse Fourier Transform maps $F$ back to $f$.

The frequency domain is useful because, in that domain:

• we can remove periodic noise by suppressing sinusoids near the frequency of the noise;
• we can perform convolution more efficiently by multiplying the Fourier transforms of the two signals, instead of convolving the two signals in the spatial domain;
• we can design spatial filters to allow only certain frequencies to be present in the signal (e.g. permitting only low frequencies results in smoothing, and permitting only high frequencies results in edge detection);
• and many other things ...

In 2D, the sinusoidal waves are waves that cross the image in different directions, with different frequencies, amplitudes, and phases.

Below are some 2D sinusoidal waves (from Steven Lehar at cns-alumni.bu.edu/~slehar/fourier/fourier.html):

And here is the sum of the second and third sinusoidal waves above:

Here is some code to generate the images above: sinusoids.py. Please try running the code with different sums of sinusoids.

The 2D Fourier Transform determines which 2D sinusoidal waves are present in an image, just as the 1D Fourier Transform determines which 1D sinusoidal waves are present in a 1D signal. But the 2D Transform considers waves in all directions across the image.

See the applet at www.falstad.com/fourier/