Reductions

The statement "$A$ can be reduced to $B$ " is written as

$$\displaystyle A \leq_P B$$

The $P$ subscript means that the reduction is done in polynomial time, which will be important later when we reduce problems in $\NP$.

The symbol $\leq_P$ conveys the idea that $A$ is no harder than $B$ or, in other words, that $B$ is at least as hard as $A$.

Consider two problems:

• Problem $A$ is to find the minimum of a set of $n$ integers.
• Problem $B$ is to sort $n$ integers.

We can reduce $A$ to $B$ by providing the same set of integers to $B$, getting it sorted, and picking the first element in the sorted order.

In this case, we have solved a simple problem by reducing it to a more complex problem.

$A$ has a lower bound of $\Omega(n)$. Since $B$ can solve $A$, $A$'s lower bound is also a lower bound for $B$ and we've proven that a lower bound for $B$ (sorting) is $\Omega(n)$.

While this is a trivial example, the key idea is that

If $A$ can be reduced to $B$, then $A$'s lower bound is also a lower bound for $B$.

Let's try a non-trivial example. Consider two problems:

• Problem $A$ is to sort $n$ integers.
• Problem $B$ is to find the convex hull of $n$ points.

We know that sorting is in $\Omega(n \log n)$. But what about convex hull?

If we could reduce sorting to convex hull, we would know that convex hull is also in $\Omega(n \log n)$.

So ... given $n$ integers to be sorted, how can we convert the integers into a set of points (i.e. the input to the convex hull problem) such that the convex hull of those points gives us the sorted order of the original integers?

And the answer is ... for each integer, $i$, to be sorted, provide a corresponding point $(i,i^2)$ to the convex hull problem.

Suppose we have the integers $\{5,1,7,2,10\}$. Then the corresponding points would be

$$\{ (5,25), (1,1), (7,49), (2,4), (10,100) \}.$$

which look like this (scaled a bit in the $y$ direction):

And their convex hull would be:

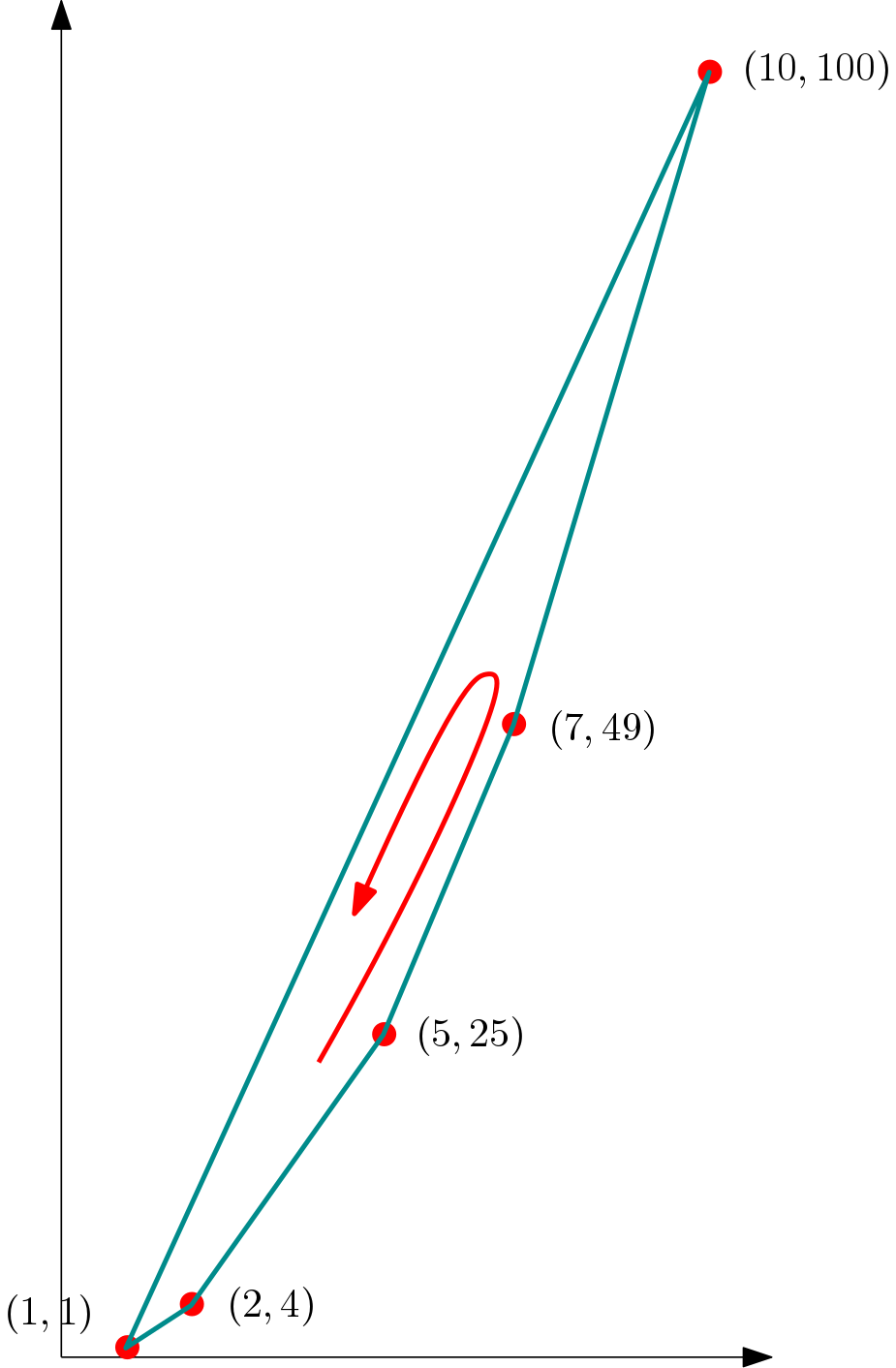
Given the convex hull, we can walk around it to gather the points in order (since the solution to the convex hull problem is an ordered set of points on the hull).

Suppose we start walking at $(5,25)$. Then the sequence of points is

$$\langle\ (5,25), (7,49), (10,100), (1,1), (2,4)\ \rangle.$$

We can extract only the $x$ components to get

$$\langle\ 5, 7, 10, 1, 4\ \rangle$$

and label those as $x_1$ to $x_n$:

$$\langle\ x_1, x_2, x_3, x_4, x_5\ \rangle$$

Then we find the index, $i$, of minimum value. In this case the minimum value is $x_4 = 1$ and its index is $i = 4$.

So the sorted sequence is

$$\langle\ x_i, x_{i+1}, \ldots x_n, x_1, x_2, \ldots, x_{i-1}\ \rangle.$$

Analysis