Memoization
The table below (from the course notes) shows in grey those
cells in table[i,j] that are filled with values when memoization
is used for the Longest Common Subsequence problem.
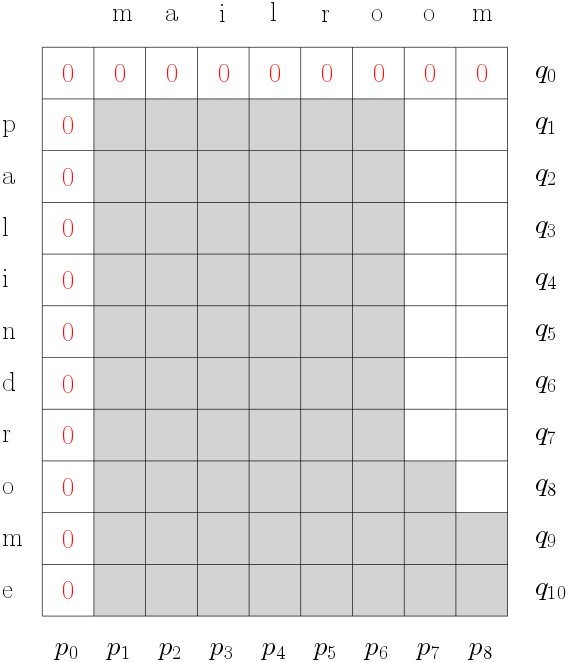
The entry at table[i,j] corresponds to characters $p_i$ and $q_j$ in the strings $p$ and $q$.
Why is no value computed in table[7,7]?
- because $p_7 \neq q_7$
- because $p_7 = q_8$
- because $p_7 = q_8$ and table[8,8] is not computed
- because $p_7 \neq q_7$ or table[8,8] is not computed
because $p_7 = q_8$ and table[8,8] is not computed
If $p_7 = q_8$, the code from [7,8] recurses diagonally only to [6,7], missing [7,7].
But [7,7] might also have been visited to from [8,7] or [8,8]. But, since [8,8] is not computed, [7,7] cannot be visited from either.
Pseudo-polynomial
A "counting sort" can sort $n$ positive numbers, the largest of which is $k$, in time ${\cal O}(n + k)$.
Why is this a pseudo-polynomial running time?
- $k$ could be as large as $n$
- $n$ could be as large as $k$
- $k$ is a value, not an input size.
- $n$ is an input size, not a value.
$k$ is a value, not an input size.
The running time is polynomial in $n$ and is polynomial in $\log_2 k$ (n the number of bits of $k$).
But the running time is pseudo-polynomail in $k$, since $k$ is a value.
Knapsack
The knapsack problem for $n$ items and maximum size $S$ can be solved with dynamic programming by filling a $(n+1) \times (S+1)$ table.
The table can be converted into a graph in which a single-source shortest path algorithm can be used to find a solution. In the graph, there is a single source node corresponding to cell $(n,S)$ of the table and there is a destination node for each cell $(0,j)$ and for each cell $(i,0)$.
How many edges are in the graph?
- exactly $2 n S$
- exactly $2 n S + n + S$
- exactly $2 (n+1) (S+1)$
- at most $2 n S$, but possibly fewer
- between $2 n S + 1$ and $2 n S + n + S$, inclusive
at most $2 n S$, but possibly fewer
Each cell $(i,j)$ in the range $[1,n] \times [1,S]$ can have one or two outgoing edges: one if only the $\mathrm{KP}(i,j)$ recursive call is made and two if both the $\mathrm{KP}(i,j)$ and $\mathrm{KP}(i,j-s_i)$ recursive calls are made.
The $\mathrm{KP}(i,j-s_i)$ recursive call is made if and only if $j-s_i \geq 0$.
The edges cells with indices $(i,0)$ and $(0,j)$ have no outgoing edges as they correspond to states where the knapsack is exactly full $(i,0)$ or where there are no items left $(0,j)$.
So there are at most $2 n S$ edges, but possible fewer.